Where On The Periodic Table Would You Expect To Find The Smallest Atoms?

This is "Sizes of Atoms and Ions", section 7.2 from the volume Principles of General Chemical science (v. one.0). For details on it (including licensing), click here.

This book is licensed under a Artistic Eatables by-nc-sa 3.0 license. See the license for more than details, but that basically means yous tin share this book as long as y'all credit the author (but see below), don't make money from information technology, and do make it available to everyone else under the same terms.

This content was attainable as of Dec 29, 2012, and it was downloaded then by Andy Schmitz in an endeavor to preserve the availability of this volume.

Normally, the author and publisher would be credited here. However, the publisher has asked for the customary Creative Commons attribution to the original publisher, authors, title, and book URI to exist removed. Additionally, per the publisher'south request, their name has been removed in some passages. More data is available on this project's attribution page.

For more than information on the source of this book, or why it is available for free, delight see the project'southward home page. You lot can browse or download boosted books there. To download a .zip file containing this book to use offline, just click here.

Has this volume helped you? Consider passing it on:

Creative Commons supports gratis civilization from music to education. Their licenses helped make this book bachelor to you lot.

DonorsChoose.org helps people like yous help teachers fund their classroom projects, from art supplies to books to calculators.

7.2 Sizes of Atoms and Ions

Learning Objectives

1. To understand periodic trends in atomic radii.
2. To predict relative ionic sizes within an isoelectronic series.

Although some people fall into the trap of visualizing atoms and ions as pocket-sized, hard spheres similar to miniature table-lawn tennis balls or marbles, the breakthrough mechanical model tells united states that their shapes and boundaries are much less definite than those images suggest. As a issue, atoms and ions cannot exist said to have verbal sizes. In this section, we discuss how diminutive and ion "sizes" are defined and obtained.

Atomic Radii

Recall from Chapter 6 "The Structure of Atoms" that the probability of finding an electron in the various available orbitals falls off slowly equally the distance from the nucleus increases. This point is illustrated in Effigy 7.4 "Plots of Radial Probability as a Function of Distance from the Nucleus for He, Ne, and Ar", which shows a plot of total electron density for all occupied orbitals for three noble gases as a office of their altitude from the nucleus. Electron density diminishes gradually with increasing distance, which makes information technology impossible to describe a abrupt line marking the purlieus of an atom.

Figure vii.four Plots of Radial Probability as a Part of Distance from the Nucleus for He, Ne, and Ar

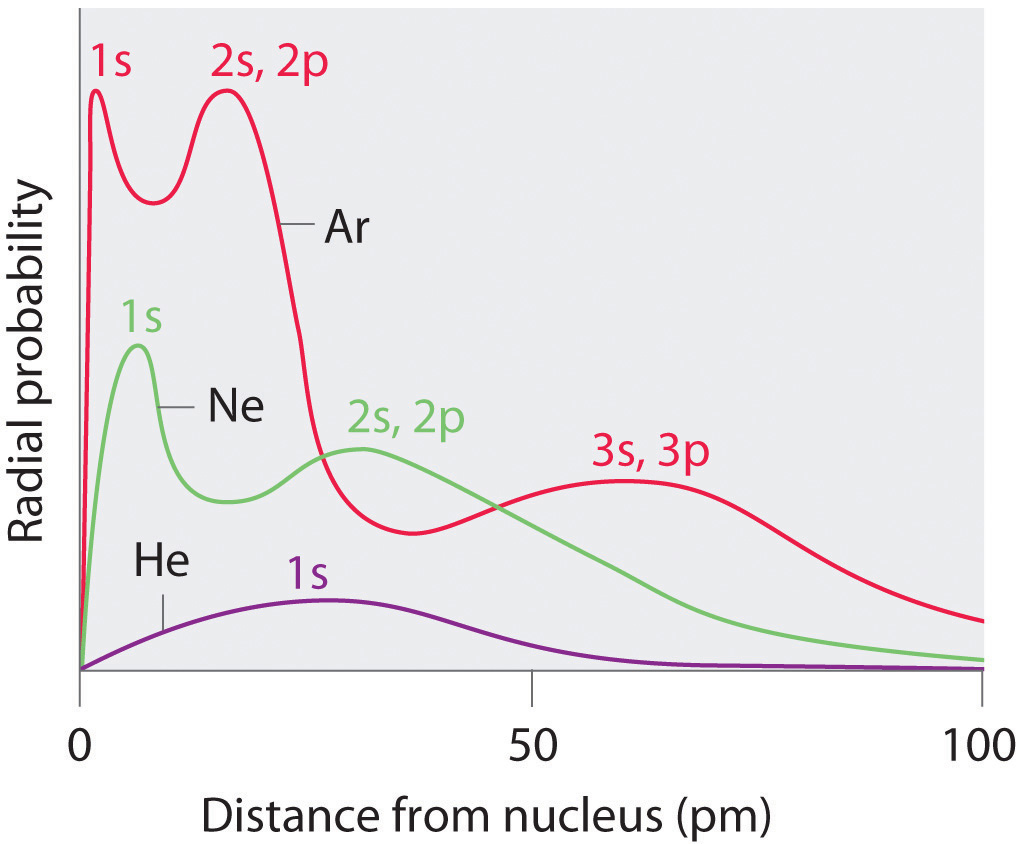
In He, the 1s electrons take a maximum radial probability at ≈30 pm from the nucleus. In Ne, the isouthward electrons have a maximum at ≈8 pm, and the iisouthward and 2p electrons combine to course another maximum at ≈35 pm (the north = ii beat out). In Ar, the anesouthward electrons take a maximum at ≈2 pm, the iis and 2p electrons combine to form a maximum at ≈18 pm, and the 3s and threep electrons combine to form a maximum at ≈70 pm.

Effigy vii.4 "Plots of Radial Probability as a Function of Distance from the Nucleus for He, Ne, and Ar" also shows that there are distinct peaks in the total electron density at particular distances and that these peaks occur at unlike distances from the nucleus for each element. Each peak in a given plot corresponds to the electron density in a given chief beat out. Because helium has only one filled vanquish (n = 1), it shows but a single peak. In dissimilarity, neon, with filled n = 1 and 2 principal shells, has two peaks. Argon, with filled due north = i, 2, and iii principal shells, has three peaks. The top for the filled n = 1 shell occurs at successively shorter distances for neon (Z = x) and argon (Z = 18) because, with a greater number of protons, their nuclei are more positively charged than that of helium. Because the anes ² shell is closest to the nucleus, its electrons are very poorly shielded by electrons in filled shells with larger values of north. Consequently, the two electrons in the n = 1 shell feel nigh the full nuclear accuse, resulting in a strong electrostatic interaction betwixt the electrons and the nucleus. The energy of the n = 1 shell also decreases tremendously (the filled 1s orbital becomes more stable) every bit the nuclear accuse increases. For similar reasons, the filled due north = 2 shell in argon is located closer to the nucleus and has a lower energy than the n = two shell in neon.

Figure 7.four "Plots of Radial Probability as a Function of Altitude from the Nucleus for He, Ne, and Ar" illustrates the difficulty of measuring the dimensions of an private atom. Because distances betwixt the nuclei in pairs of covalently bonded atoms can be measured quite precisely, however, chemists utilise these distances as a basis for describing the approximate sizes of atoms. For example, the internuclear distance in the diatomic Cl₂ molecule is known to be 198 pm. We assign half of this distance to each chlorine atom, giving chlorine a covalent atomic radius (r _cov)Half the altitude between the nuclei of 2 like atoms joined by a covalent bail in the same molecule. of 99 pm or 0.99 Å (part (a) in Figure 7.5 "Definitions of the Diminutive Radius").Diminutive radii are oftentimes measured in angstroms (Å), a non-SI unit: ane Å = 1 × 10⁻¹⁰ thousand = 100 pm.

Effigy 7.five Definitions of the Atomic Radius

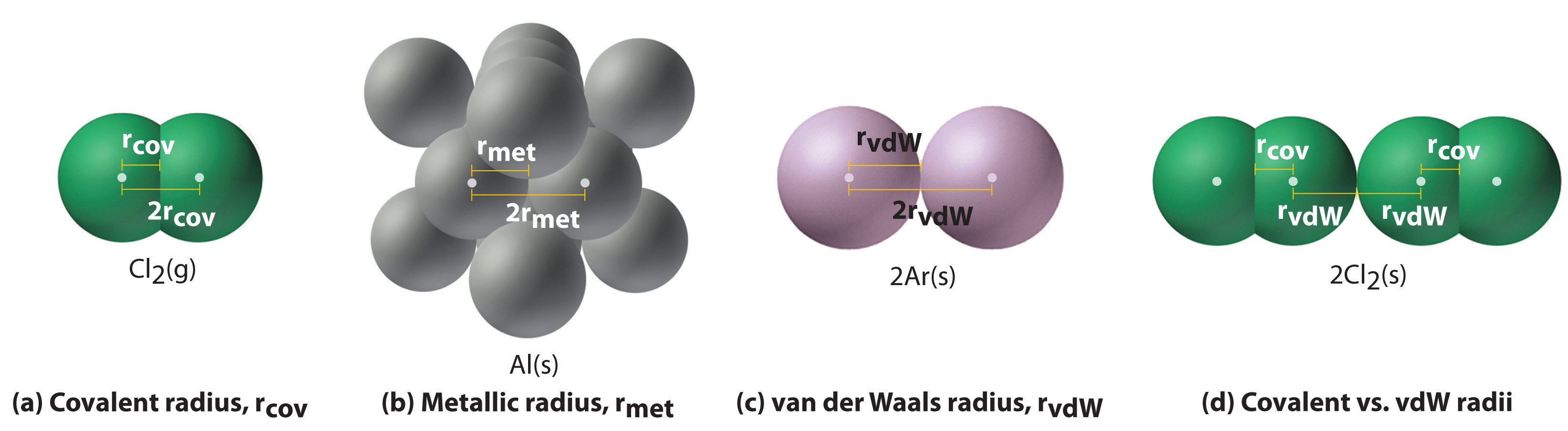
(a) The covalent atomic radius, r _cov, is half the distance between the nuclei of ii like atoms joined by a covalent bond in the same molecule, such as Cl₂. (b) The metallic atomic radius, r _met, is half the distance between the nuclei of two adjacent atoms in a pure solid metallic, such as aluminum. (c) The van der Waals atomic radius, r _vdW, is half the distance between the nuclei of ii like atoms, such equally argon, that are closely packed just non bonded. (d) This is a depiction of covalent versus van der Waals radii of chlorine.

In a similar approach, nosotros can use the lengths of carbon–carbon single bonds in organic compounds, which are remarkably compatible at 154 pm, to assign a value of 77 pm equally the covalent atomic radius for carbon. If these values do indeed reverberate the actual sizes of the atoms, and so we should exist able to predict the lengths of covalent bonds formed between unlike elements by calculation them. For example, we would predict a carbon–chlorine altitude of 77 pm + 99 pm = 176 pm for a C–Cl bond, which is very close to the boilerplate value observed in many organochlorine compounds.A similar approach for measuring the size of ions is discussed later in this section.

Covalent atomic radii can be adamant for near of the nonmetals, just how practice chemists obtain atomic radii for elements that do not form covalent bonds? For these elements, a variety of other methods have been developed. With a metal, for example, the metallic diminutive radius(r _met)Half the distance betwixt the nuclei of two side by side metal atoms. is divers equally half the distance between the nuclei of two adjacent metallic atoms (part (b) in Figure vii.5 "Definitions of the Atomic Radius"). For elements such equally the noble gases, most of which form no stable compounds, we can apply what is chosen the van der Waals atomic radius(r _vdW)Half the internuclear distance between two nonbonded atoms in the solid. , which is half the internuclear distance between two nonbonded atoms in the solid (office (c) in Figure 7.5 "Definitions of the Atomic Radius"). An cantlet such as chlorine has both a covalent radius (the distance between the 2 atoms in a Cl_ii molecule) and a van der Waals radius (the distance between two Cl atoms in different molecules in, for instance, Cl₂(southward) at low temperatures). These radii are mostly non the same (part (d) in Figure vii.5 "Definitions of the Atomic Radius").

Periodic Trends in Atomic Radii

Because it is impossible to measure out the sizes of both metal and nonmetallic elements using any i method, chemists have developed a self-consequent manner of calculating diminutive radii using the breakthrough mechanical functions described in Affiliate 6 "The Structure of Atoms". Although the radii values obtained past such calculations are not identical to whatever of the experimentally measured sets of values, they practice provide a way to compare the intrinsic sizes of all the elements and conspicuously show that atomic size varies in a periodic fashion (Effigy vii.6 "A Plot of Periodic Variation of Diminutive Radius with Diminutive Number for the First Six Rows of the Periodic Tabular array"). In the periodic table, diminutive radii decrease from left to right across a row and increment from top to lesser down a cavalcade. Because of these ii trends, the largest atoms are found in the lower left corner of the periodic tabular array, and the smallest are plant in the upper correct corner (Effigy 7.7 "Calculated Diminutive Radii (in Picometers) of the ").

Effigy 7.vii Calculated Atomic Radii (in Picometers) of the s-, p-, and d-Cake Elements

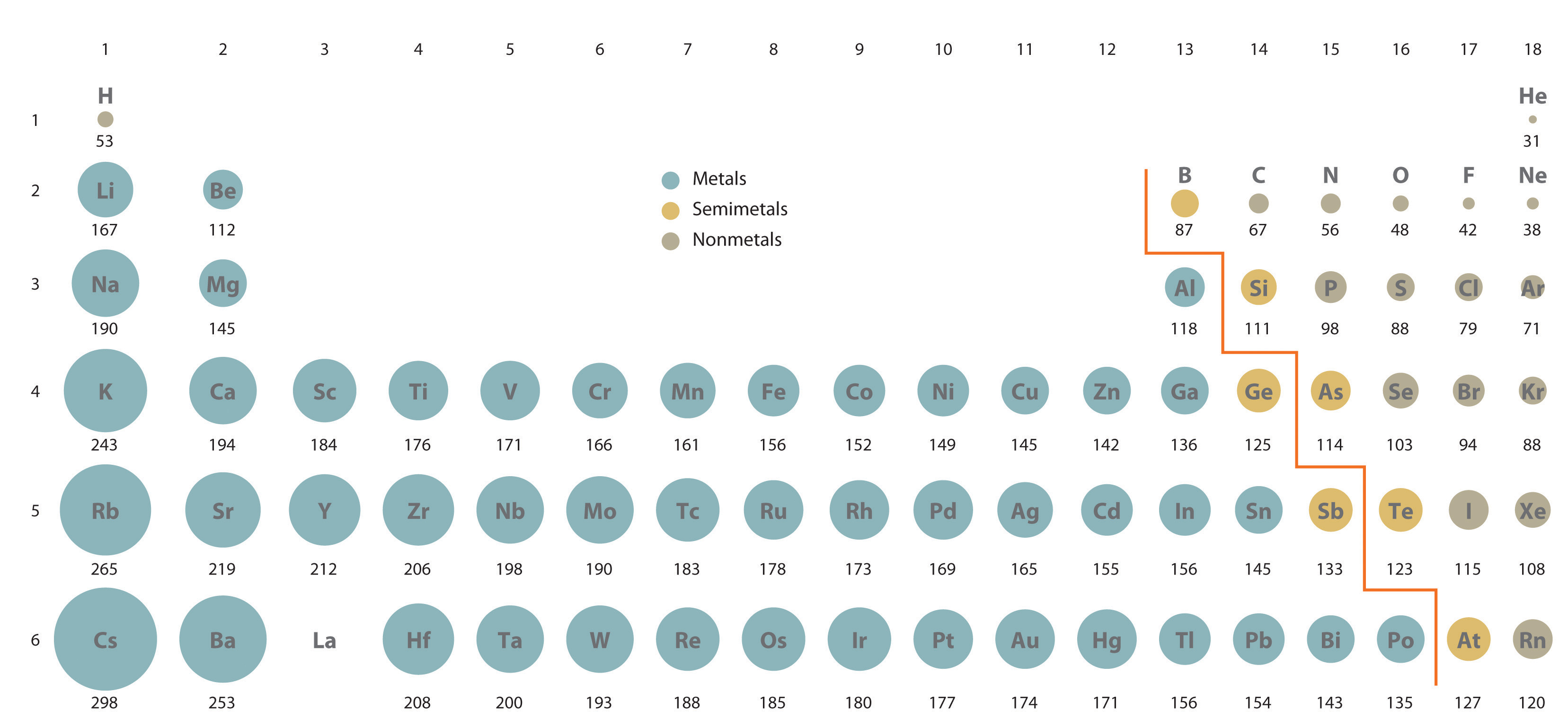
The sizes of the circles illustrate the relative sizes of the atoms. The calculated values are based on breakthrough mechanical wave functions.

Note the Blueprint

Atomic radii decrease from left to correct beyond a row and increment from top to bottom down a column.

Trends in atomic size event from differences in the effective nuclear charges ( Z _eff ) experienced by electrons in the outermost orbitals of the elements. Every bit we described in Affiliate 6 "The Structure of Atoms", for all elements except H, the effective nuclear charge is always less than the actual nuclear charge because of shielding effects. The greater the effective nuclear charge, the more strongly the outermost electrons are attracted to the nucleus and the smaller the atomic radius.

The atoms in the second row of the periodic table (Li through Ne) illustrate the issue of electron shielding. (For more information on electron shielding, see Chapter half-dozen "The Structure of Atoms", Department 6.5 "Atomic Orbitals and Their Energies", and Figure vi.29 "Orbital Free energy Level Diagram for a Typical Multielectron Atom".) All have a filled anes ⁱⁱ inner crush, simply as we go from left to right across the row, the nuclear charge increases from +3 to +10. Although electrons are being added to the 2s and 2p orbitals, electrons in the same principal trounce are not very constructive at shielding one another from the nuclear accuse. Thus the single 2south electron in lithium experiences an effective nuclear charge of approximately +1 considering the electrons in the filled onesouth ^two shell effectively neutralize two of the three positive charges in the nucleus. (More detailed calculations give a value of Z _eff = +one.26 for Li.) In dissimilarity, the two 2south electrons in beryllium do not shield each other very well, although the filled onesouth ² shell finer neutralizes two of the four positive charges in the nucleus. This means that the effective nuclear charge experienced by the 2s electrons in beryllium is between +1 and +2 (the calculated value is +one.66). Consequently, beryllium is significantly smaller than lithium. Similarly, as nosotros proceed across the row, the increasing nuclear accuse is not effectively neutralized by the electrons being added to the 2southward and 2p orbitals. The upshot is a steady increment in the effective nuclear charge and a steady decrease in atomic size.

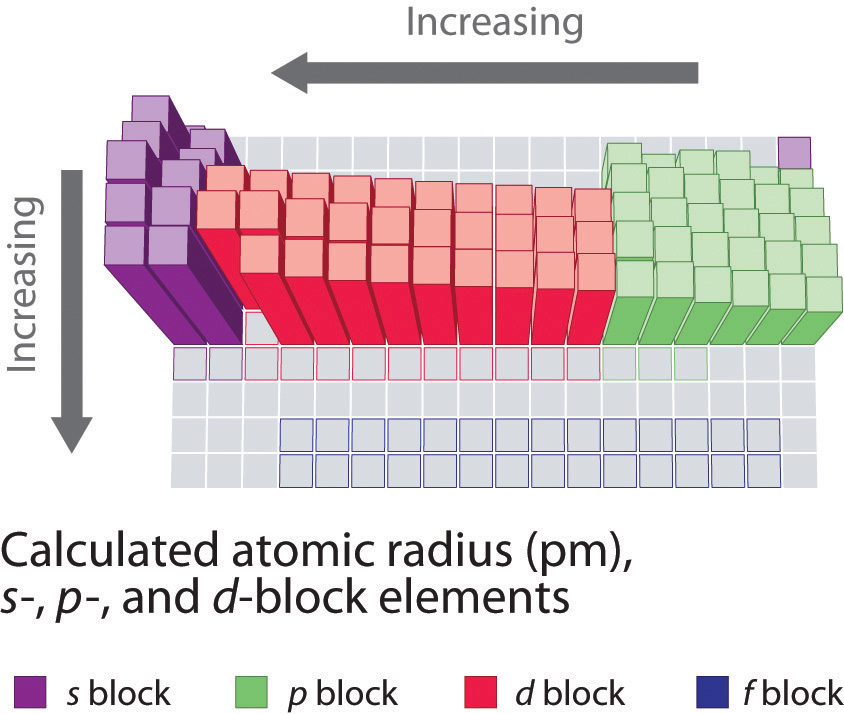
The increase in atomic size going down a column is also due to electron shielding, but the situation is more than complex because the main quantum number northward is not abiding. As we saw in Chapter 6 "The Structure of Atoms", the size of the orbitals increases as n increases, provided the nuclear charge remains the same. In group 1, for example, the size of the atoms increases substantially going downward the column. It may at kickoff seem reasonable to attribute this effect to the successive addition of electrons to ns orbitals with increasing values of north. Yet, it is of import to remember that the radius of an orbital depends dramatically on the nuclear accuse. As nosotros go downwardly the column of the grouping one elements, the principal quantum number north increases from 2 to six, but the nuclear charge increases from +3 to +55! If the outermost electrons in cesium experienced the full nuclear charge of +55, a cesium atom would exist very minor indeed. In fact, the effective nuclear charge felt past the outermost electrons in cesium is much less than expected (half-dozen rather than 55). This means that cesium, with a vis ¹ valence electron configuration, is much larger than lithium, with a 2s ^ane valence electron configuration. The effective nuclear charge changes relatively little from lithium to cesium because electrons in filled inner shells are highly effective at shielding electrons in outer shells from the nuclear charge. Even though cesium has a nuclear charge of +55, it has 54 electrons in its filled 1s ^twotwos ²2p ⁶3s ²iiip ^viivs ²3d ¹⁰4p ^six5s ⁱⁱ4d ^x5p ⁶ shells, abbreviated as [Xe]5s ⁱⁱ4d ^tenfivep ^six, which effectively neutralize nigh of the 55 positive charges in the nucleus. The same dynamic is responsible for the steady increase in size observed equally we become downward the other columns of the periodic tabular array. Irregularities tin can usually exist explained by variations in effective nuclear accuse.

Annotation the Pattern

Electrons in the same primary shell are non very effective at shielding one another from the nuclear charge, whereas electrons in filled inner shells are highly effective at shielding electrons in outer shells from the nuclear charge.

Case ii

On the basis of their positions in the periodic tabular array, arrange these elements in order of increasing atomic radius: aluminum, carbon, and silicon.

Given: three elements

Asked for: arrange in order of increasing atomic radius

Strategy:

A Identify the location of the elements in the periodic table. Make up one's mind the relative sizes of elements located in the same column from their principal quantum number n. So determine the gild of elements in the same row from their constructive nuclear charges. If the elements are not in the same column or row, use pairwise comparisons.

B List the elements in order of increasing atomic radius.

Solution:

A These elements are not all in the same column or row, so we must use pairwise comparisons. Carbon and silicon are both in grouping 14 with carbon lying above, so carbon is smaller than silicon (C < Si). Aluminum and silicon are both in the third row with aluminum lying to the left, then silicon is smaller than aluminum (Si < Al) because its effective nuclear charge is greater. B Combining the 2 inequalities gives the overall order: C < Si < Al.

Do

On the footing of their positions in the periodic table, arrange these elements in order of increasing size: oxygen, phosphorus, potassium, and sulfur.

Answer: O < Southward < P < K

Ionic Radii and Isoelectronic Serial

As you learned in Chapter 2 "Molecules, Ions, and Chemical Formulas", ionic compounds consist of regular repeating arrays of alternating cations and anions. Although it is not possible to mensurate an ionic radius direct for the same reason it is non possible to straight measure out an atom'south radius, it is possible to measure the distance between the nuclei of a cation and an adjacent anion in an ionic compound to determine the ionic radiusThe radius of a cation or anion. of i or both. As illustrated in Figure 7.8 "Definition of Ionic Radius", the internuclear distance corresponds to the sum of the radii of the cation and anion. A variety of methods have been developed to split the experimentally measured distance proportionally between the smaller cation and larger anion. These methods produce sets of ionic radii that are internally consistent from i ionic chemical compound to another, although each method gives slightly different values. For example, the radius of the Na⁺ ion is essentially the aforementioned in NaCl and Na₂Due south, as long every bit the aforementioned method is used to measure it. Thus despite minor differences due to methodology, certain trends tin be observed.

Figure 7.viii Definition of Ionic Radius

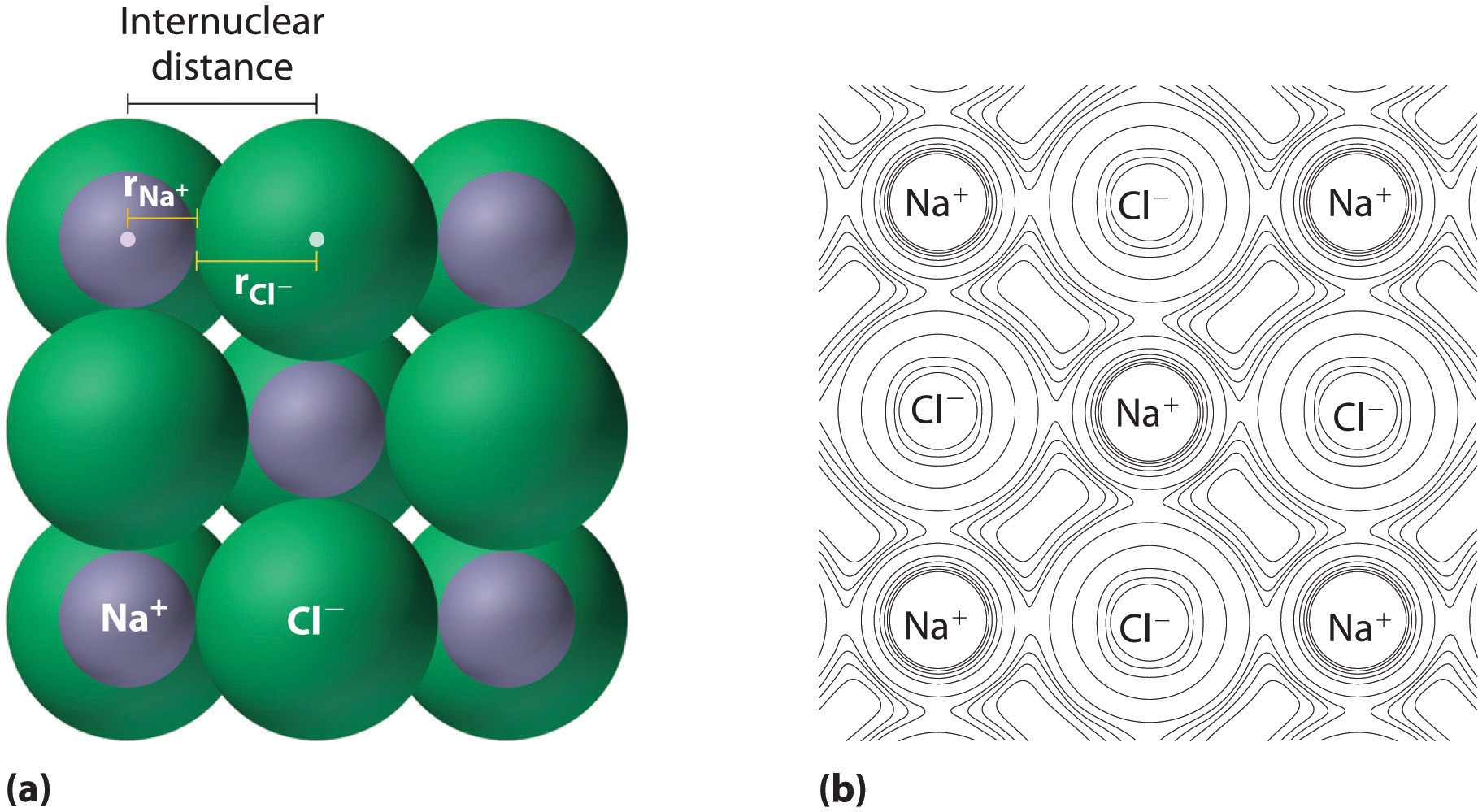
(a) The internuclear distance is apportioned between adjacent cations and anions in the ionic structure, every bit shown here for Na⁺ and Cl⁻ in sodium chloride. (b) This depiction of electron density contours for a single plane of atoms in the NaCl structure shows how the lines connect points of equal electron density. Note the relative sizes of the electron density contour lines around Cl⁻ and Na⁺.

A comparison of ionic radii with diminutive radii (Figure 7.9 "Ionic Radii (in Picometers) of the Most Mutual Oxidation States of the ") shows that a cation is always smaller than its parent neutral atom, and an anion is always larger than the parent neutral atom. When 1 or more electrons is removed from a neutral atom, ii things happen: (1) repulsions between electrons in the aforementioned principal shell decrease considering fewer electrons are present, and (2) the constructive nuclear charge felt past the remaining electrons increases because at that place are fewer electrons to shield one another from the nucleus. Consequently, the size of the region of space occupied by electrons decreases (compare Li at 167 pm with Li⁺ at 76 pm). If different numbers of electrons can be removed to produce ions with different charges, the ion with the greatest positive charge is the smallest (compare Fe²⁺ at 78 pm with Fe³⁺ at 64.5 pm). Conversely, adding one or more electrons to a neutral atom causes electron–electron repulsions to increase and the constructive nuclear charge to decrease, so the size of the probability region increases (compare F at 42 pm with F⁻ at 133 pm).

Figure vii.nine Ionic Radii (in Picometers) of the Nearly Common Oxidation States of the s-, p-, and d-Block Elements

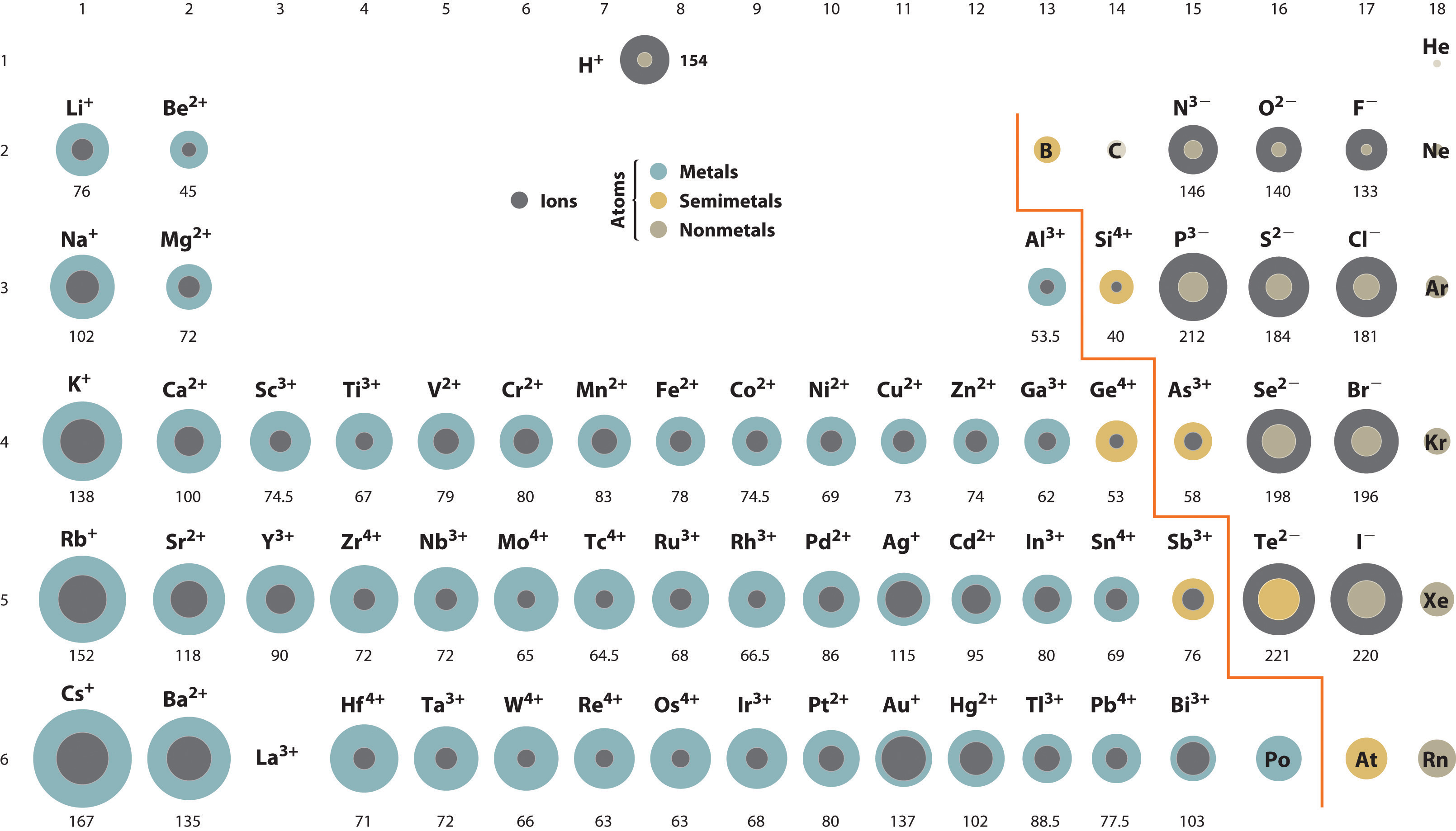
Grayness circles bespeak the sizes of the ions shown; colored circles signal the sizes of the neutral atoms, previously shown in Figure 7.7 "Calculated Atomic Radii (in Picometers) of the ".

Source: Ionic radius data from R. D. Shannon, "Revised constructive ionic radii and systematic studies of interatomic distances in halides and chalcogenides," Acta Crystallographica 32, no. 5 (1976): 751–767.

Note the Pattern

Cations are e'er smaller than the neutral atom, and anions are always larger.

Considering most elements form either a cation or an anion but not both, at that place are few opportunities to compare the sizes of a cation and an anion derived from the same neutral cantlet. A few compounds of sodium, yet, contain the Na⁻ ion, allowing comparing of its size with that of the far more than familiar Na⁺ ion, which is constitute in many compounds. The radius of sodium in each of its iii known oxidation states is given in Tabular array 7.2 "Experimentally Measured Values for the Radius of Sodium in Its 3 Known Oxidation States". All three species take a nuclear charge of +xi, but they contain 10 (Na⁺), 11 (Na⁰), and 12 (Na⁻) electrons. The Na⁺ ion is significantly smaller than the neutral Na atom because the 3s ¹ electron has been removed to give a closed trounce with northward = 2. The Na⁻ ion is larger than the parent Na atom considering the additional electron produces a threes ² valence electron configuration, while the nuclear charge remains the aforementioned.

Table 7.2 Experimentally Measured Values for the Radius of Sodium in Its Three Known Oxidation States

	Na+	Na0	Na−
Electron Configuration	is twoiis 22p half dozen	anes two2s two2p viiiidue south 1	onesouthward 22due south 2iip half dozen3south 2
Radius (pm)	102	154*	202†
*The metal radius measured for Na(s).
†Source: M. J. Wagner and J. L. Dye, "Alkalides, Electrides, and Expanded Metals," Almanac Review of Materials Science 23 (1993): 225–253.

Ionic radii follow the same vertical trend every bit atomic radii; that is, for ions with the same charge, the ionic radius increases going down a column. The reason is the aforementioned equally for atomic radii: shielding by filled inner shells produces little modify in the effective nuclear charge felt past the outermost electrons. Again, principal shells with larger values of north lie at successively greater distances from the nucleus.

Because elements in different columns tend to form ions with unlike charges, information technology is not possible to compare ions of the aforementioned charge across a row of the periodic table. Instead, elements that are adjacent to each other tend to form ions with the aforementioned number of electrons just with dissimilar overall charges because of their unlike atomic numbers. Such a set of species is known equally an isoelectronic seriesA group of ions or atoms and ions that have the same number of electrons and thus the same ground-state electron configuration. . For example, the isoelectronic series of species with the neon closed-crush configuration (1s ²2s ²2p ⁶) is shown in Table 7.3 "Radius of Ions with the Neon Closed-Beat out Electron Configuration". The sizes of the ions in this serial decrease smoothly from Due north^three− to Al³⁺. All six of the ions contain 10 electrons in the ones, twos, and twop orbitals, simply the nuclear charge varies from +vii (Due north) to +13 (Al). Every bit the positive accuse of the nucleus increases while the number of electrons remains the same, there is a greater electrostatic attraction between the electrons and the nucleus, which causes a decrease in radius. Consequently, the ion with the greatest nuclear accuse (Al³⁺) is the smallest, and the ion with the smallest nuclear charge (N³⁻) is the largest. One fellow member of this isoelectronic serial is non listed in Table 7.3 "Radius of Ions with the Neon Closed-Shell Electron Configuration": the neon atom. Considering neon forms no covalent or ionic compounds, its radius is difficult to measure.

Table 7.3 Radius of Ions with the Neon Closed-Vanquish Electron Configuration

Ion	Radius (pm)	Atomic Number
North3−	146	7
Otwo−	140	8
F−	133	9
Na+	102	11
Mg2+	72	12
Al3+	53.5	13

Source: R. D. Shannon, "Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides," Acta Crystallographica 32, no. five (1976): 751–767.

Example 3

Based on their positions in the periodic table, adjust these ions in order of increasing radius: Cl⁻, K⁺, Southⁱⁱ⁻, and Se^two−.

Given: iv ions

Asked for: guild by increasing radius

Strategy:

A Make up one's mind which ions form an isoelectronic series. Of those ions, predict their relative sizes based on their nuclear charges. For ions that do not grade an isoelectronic series, locate their positions in the periodic table.

B Determine the relative sizes of the ions based on their principal quantum numbers n and their locations within a row.

Solution:

A We see that S and Cl are at the correct of the third row, while One thousand and Se are at the far left and right ends of the fourth row, respectively. Thousand⁺, Cl⁻, and Due south²⁻ class an isoelectronic series with the [Ar] closed-shell electron configuration; that is, all three ions contain 18 electrons but have different nuclear charges. Because K⁺ has the greatest nuclear accuse (Z = xix), its radius is smallest, and S²⁻ with Z = 16 has the largest radius. Because selenium is directly beneath sulfur, we await the Se^two− ion to exist fifty-fifty larger than S²⁻. B The order must therefore exist Grand⁺ < Cl⁻ < S^two− < Se²⁻.

Exercise

Based on their positions in the periodic table, adapt these ions in guild of increasing size: Br⁻, Ca²⁺, Rb⁺, and Sr²⁺.

Reply: Ca²⁺ < Sr²⁺ < Rb⁺ < Br⁻

Summary

A variety of methods have been established to measure out the size of a single cantlet or ion. The covalent atomic radius ( r _cov ) is half the internuclear distance in a molecule with two identical atoms bonded to each other, whereas the metallic atomic radius ( r _met ) is divers as one-half the distance between the nuclei of two adjacent atoms in a metallic element. The van der Waals radius ( r _vdW ) of an element is half the internuclear distance between 2 nonbonded atoms in a solid. Atomic radii decrease from left to correct beyond a row because of the increase in effective nuclear charge due to poor electron screening by other electrons in the same main beat. Moreover, diminutive radii increase from acme to bottom down a column because the constructive nuclear charge remains relatively abiding as the principal quantum number increases. The ionic radii of cations and anions are ever smaller or larger, respectively, than the parent cantlet due to changes in electron–electron repulsions, and the trends in ionic radius parallel those in atomic size. A comparing of the dimensions of atoms or ions that have the same number of electrons only different nuclear charges, chosen an isoelectronic serial, shows a clear correlation between increasing nuclear charge and decreasing size.

Fundamental Takeaway

• Ionic radii share the same vertical trend as diminutive radii, but the horizontal trends differ due to differences in ionic charges.

Conceptual Problems

1. The electrons of the 1southward shell have a stronger electrostatic attraction to the nucleus than electrons in the iis shell. Requite 2 reasons for this.

2. Predict whether Na or Cl has the more stable 1s ² shell and explicate your rationale.

3. Arrange M, F, Ba, Pb, B, and I in order of decreasing diminutive radius.

4. Arrange Ag, Pt, Mg, C, Cu, and Si in order of increasing atomic radius.

5. Using the periodic table, adjust Li, Ga, Ba, Cl, and Ni in club of increasing atomic radius.

6. Element M is a metal that forms compounds of the type MX₂, MX₃, and MX_iv, where X is a halogen. What is the expected tendency in the ionic radius of M in these compounds? Arrange these compounds in order of decreasing ionic radius of M.

7. The diminutive radii of Na and Cl are 190 and 79 pm, respectively, only the distance between sodium and chlorine in NaCl is 282 pm. Explicate this discrepancy.

8. Are shielding effects on the atomic radius more pronounced across a row or downwards a grouping? Why?

9. What two factors influence the size of an ion relative to the size of its parent atom? Would yous expect the ionic radius of S²⁻ to exist the same in both MgS and Na₂S? Why or why not?

10. Adapt Br⁻, Alⁱⁱⁱ⁺, Sr²⁺, F⁻, Oⁱⁱ⁻, and I⁻ in order of increasing ionic radius.

11. Adjust P³⁻, Due north³⁻, Cl⁻, In³⁺, and S²⁻ in club of decreasing ionic radius.

12. How is an isoelectronic series different from a series of ions with the same charge? Practice the cations in magnesium, strontium, and potassium sulfate course an isoelectronic series? Why or why non?

13. What isoelectronic series arises from fluorine, nitrogen, magnesium, and carbon? Suit the ions in this series by

    1. increasing nuclear accuse.
    2. increasing size.

14. What would be the charge and electron configuration of an ion formed from calcium that is isoelectronic with

    1. a chloride ion?
    2. Ar⁺?

Answers

1. The 1due south shell is closer to the nucleus and therefore experiences a greater electrostatic attraction. In improver, the electrons in the 2southward subshell are shielded by the filled is ^two beat out, which further decreases the electrostatic attraction to the nucleus.

3. Ba > K > Atomic number 82 > I > B > F

7. The sum of the calculated atomic radii of sodium and chlorine atoms is 253 pm. The sodium cation is significantly smaller than a neutral sodium atom (102 versus 154 pm), due to the loss of the single electron in the 3due south orbital. Conversely, the chloride ion is much larger than a neutral chlorine atom (181 versus 99 pm), because the added electron results in greatly increased electron–electron repulsions within the filled due north = 3 master shell. Thus, transferring an electron from sodium to chlorine decreases the radius of sodium by well-nigh l%, simply causes the radius of chlorine to most double. The net result is that the distance between a sodium ion and a chloride ion in NaCl is greater than the sum of the diminutive radii of the neutral atoms.

Numerical Bug

1. Plot the ionic charge versus ionic radius using the post-obit data for Mo: Mo³⁺, 69 pm; Mo⁴⁺, 65 pm; and Mo⁵⁺, 61 pm. Then use this plot to predict the ionic radius of Mo⁶⁺. Is the observed trend consistent with the general trends discussed in the affiliate? Why or why not?

2. Internuclear distances for selected ionic compounds are given in the post-obit table.

   1. If the ionic radius of Li⁺ is 76 pm, what is the ionic radius of each of the anions?

      	LiF	LiCl	LiBr	LiI
      Altitude (pm)	209	257	272	296

   2. What is the ionic radius of Na⁺?

      	NaF	NaCl	NaBr	NaI
      Distance (pm)	235	282	298	322

3. Arrange the gaseous species Mgⁱⁱ⁺, P^three−, Br⁻, South²⁻, F⁻, and N³⁻ in club of increasing radius and justify your decisions.

Source: https://2012books.lardbucket.org/books/principles-of-general-chemistry-v1.0/s11-02-sizes-of-atoms-and-ions.html

Posted by: fullerondowde.blogspot.com

Share this post