How To Find The Expected Value Of A Probability Distribution
Discrete Random Variables
Mean or Expected Value and Standard Deviation
The expected value is oftentimes referred to every bit the "long-term" average or hateful. This means that over the long term of doing an experiment over and over, you would wait this average.
You toss a coin and tape the upshot. What is the probability that the outcome is heads? If you lot flip a coin two times, does probability tell y'all that these flips will upshot in one heads and one tail? You lot might toss a fair money ten times and record nine heads. Equally you learned in (Figure), probability does non draw the brusque-term results of an experiment. It gives information about what can be expected in the long term. To demonstrate this, Karl Pearson in one case tossed a fair coin 24,000 times! He recorded the results of each toss, obtaining heads 12,012 times. In his experiment, Pearson illustrated the Law of Big Numbers.
The Constabulary of Large Numbers states that, as the number of trials in a probability experiment increases, the departure between the theoretical probability of an result and the relative frequency approaches zero (the theoretical probability and the relative frequency get closer and closer together). When evaluating the long-term results of statistical experiments, we oft want to know the "average" event. This "long-term average" is known as the hateful or expected value of the experiment and is denoted by the Greek letter μ. In other words, after conducting many trials of an experiment, you would expect this boilerplate value.
NOTE
To notice the expected value or long term boilerplate, μ, simply multiply each value of the random variable by its probability and add the products.
A men's soccer squad plays soccer zip, one, or 2 days a week. The probability that they play zero days is 0.2, the probability that they play i day is 0.five, and the probability that they play two days is 0.3. Notice the long-term average or expected value, μ, of the number of days per calendar week the men's soccer squad plays soccer.
To do the problem, get-go let the random variable X = the number of days the men'southward soccer team plays soccer per week. 10 takes on the values 0, one, 2. Construct a PDF table adding a column ten*P(x). In this column, yous will multiply each ten value by its probability.
| x | P(10) | x*P(x) |
|---|---|---|
| 0 | 0.two | (0)(0.2) = 0 |
| 1 | 0.5 | (1)(0.5) = 0.5 |
| ii | 0.iii | (2)(0.3) = 0.6 |
Add the final column ten*P(ten) to discover the long term average or expected value: (0)(0.ii) + (1)(0.5) + (2)(0.three) = 0 + 0.5 + 0.6 = 1.1.
The expected value is 1.1. The men's soccer squad would, on the average, wait to play soccer 1.1 days per week. The number 1.1 is the long-term average or expected value if the men's soccer team plays soccer week after calendar week after week. Nosotros say μ = 1.i.
Find the expected value of the number of times a newborn baby's crying wakes its mother after midnight. The expected value is the expected number of times per week a newborn baby'south crying wakes its mother after midnight. Summate the standard deviation of the variable as well.
| ten | P(x) | x*P(x) | (x – μ)2 ⋅ P(10) |
|---|---|---|---|
| 0 | P(ten = 0) = | (0) | (0 – ii.1)2 ⋅ 0.04 = 0.1764 |
| ane | P(x = i) = | (ane) | (1 – 2.1)2 ⋅ 0.22 = 0.2662 |
| 2 | P(x = 2) = | (2) | (ii – two.1)ii ⋅ 0.46 = 0.0046 |
| 3 | P(10 = three) = | (3) | (3 – 2.1)ii ⋅ 0.18 = 0.1458 |
| 4 | P(x = 4) = | (4) | (iv – ii.i)2 ⋅ 0.08 = 0.2888 |
| 5 | P(x = 5) = | (v) | (five – ii.ane)2 ⋅ 0.02 = 0.1682 |
Add the values in the third column of the table to find the expected value of X:
μ = Expected Value = ![]() = 2.i
= 2.i
Apply μ to complete the table. The fourth column of this table will provide the values you need to calculate the standard deviation. For each value x, multiply the square of its deviation by its probability. (Each deviation has the format x – μ).
Add the values in the quaternary cavalcade of the table:
0.1764 + 0.2662 + 0.0046 + 0.1458 + 0.2888 + 0.1682 = 1.05
The standard deviation of X is the square root of this sum: σ = ![]() ≈ one.0247
≈ one.0247
The mean, μ, of a detached probability function is the expected value.
![]()
The standard divergence, Σ, of the PDF is the foursquare root of the variance.
![]()
When all outcomes in the probability distribution are every bit likely, these formulas coincide with the mean and standard deviation of the set of possible outcomes.
Suppose you play a game of chance in which 5 numbers are chosen from 0, 1, 2, 3, 4, 5, half dozen, 7, 8, 9. A computer randomly selects five numbers from nil to nine with replacement. You pay ?2 to play and could profit ?100,000 if you lot match all five numbers in gild (you lot get your ?two back plus ?100,000). Over the long term, what is your expected profit of playing the game?
To do this trouble, set upwards an expected value table for the amount of money you can turn a profit.
Permit X = the amount of money y'all profit. The values of x are non 0, ane, two, 3, iv, 5, 6, 7, 8, 9. Since you are interested in your turn a profit (or loss), the values of x are 100,000 dollars and −2 dollars.
To win, you must get all v numbers correct, in order. The probability of choosing one correct number is ![]() because there are ten numbers. Y'all may cull a number more than than once. The probability of choosing all five numbers correctly and in order is
because there are ten numbers. Y'all may cull a number more than than once. The probability of choosing all five numbers correctly and in order is
![]()
Therefore, the probability of winning is 0.00001 and the probability of losing is
![]()
The expected value table is as follows:
| x | P(x) | ten*P(x) | |
|---|---|---|---|
| Loss | –2 | 0.99999 | (–2)(0.99999) = –ane.99998 |
| Profit | 100,000 | 0.00001 | (100000)(0.00001) = 1 |
Since –0.99998 is most –ane, you would, on average, expect to lose approximately ?1 for each game you play. However, each time you play, you either lose ?2 or profit ?100,000. The ?1 is the average or expected LOSS per game after playing this game over and over.
Effort Information technology
Y'all are playing a game of run a risk in which four cards are drawn from a standard deck of 52 cards. You lot guess the suit of each card earlier it is drawn. The cards are replaced in the deck on each depict. You lot pay ?1 to play. If yous approximate the correct accommodate every time, you get your money back and ?256. What is your expected turn a profit of playing the game over the long term?
Suppose yous play a game with a biased money. Yous play each game by tossing the coin once. P(heads) = ![]() and P(tails) =
and P(tails) = ![]() . If you toss a head, you pay ?half dozen. If y'all toss a tail, yous win ?10. If you play this game many times, will you lot come out alee?
. If you toss a head, you pay ?half dozen. If y'all toss a tail, yous win ?10. If you play this game many times, will you lot come out alee?
a. Ascertain a random variable X.
b. Complete the post-obit expected value tabular array.
| 10 | ____ | ____ | |
|---|---|---|---|
| WIN | x | | ____ |
| LOSE | ____ | ____ | |
b.
| x | P(x) | xP(x) | |
|---|---|---|---|
| WIN | 10 | | |
| LOSE | –6 | | |
c. What is the expected value, μ? Practice you lot come out ahead?
c. Add together the last column of the table. The expected value μ = ![]() . You lose, on average, almost 67 cents each time you lot play the game so you do non come out ahead.
. You lose, on average, almost 67 cents each time you lot play the game so you do non come out ahead.
Like data, probability distributions accept standard deviations. To calculate the standard difference (σ) of a probability distribution, find each divergence from its expected value, foursquare it, multiply it by its probability, add the products, and take the foursquare root. To understand how to do the adding, look at the table for the number of days per calendar week a men'south soccer team plays soccer. To find the standard deviation, add together the entries in the cavalcade labeled (ten – μ)two P(x) and take the square root.
| ten | P(x) | x*P(ten) | (x – μ)2 P(x) |
|---|---|---|---|
| 0 | 0.ii | (0)(0.2) = 0 | (0 – ane.1)2(0.2) = 0.242 |
| ane | 0.5 | (1)(0.5) = 0.5 | (ane – i.one)two(0.5) = 0.005 |
| 2 | 0.3 | (2)(0.3) = 0.6 | (2 – one.1)2(0.3) = 0.243 |
Add the concluding column in the tabular array. 0.242 + 0.005 + 0.243 = 0.490. The standard deviation is the square root of 0.49, or σ = ![]() = 0.7
= 0.7
Generally for probability distributions, we use a estimator or a computer to calculate μ and σ to reduce roundoff mistake. For some probability distributions, there are brusque-cutting formulas for calculating μ and σ.
Toss a fair, six-sided die twice. Let X = the number of faces that show an fifty-fifty number. Construct a table like (Figure) and summate the mean μ and standard deviation σ of Ten.
Tossing i fair 6-sided dice twice has the same sample infinite as tossing two off-white half-dozen-sided dice. The sample space has 36 outcomes:
| (1, one) | (1, 2) | (ane, iii) | (1, four) | (1, 5) | (ane, 6) |
| (2, ane) | (ii, 2) | (2, 3) | (ii, 4) | (2, 5) | (2, 6) |
| (3, i) | (iii, 2) | (3, 3) | (3, 4) | (3, 5) | (three, 6) |
| (4, 1) | (4, ii) | (iv, 3) | (4, 4) | (4, 5) | (4, six) |
| (v, ane) | (5, 2) | (5, iii) | (5, iv) | (5, 5) | (v, 6) |
| (half dozen, 1) | (six, 2) | (six, iii) | (half dozen, four) | (6, 5) | (6, 6) |
Use the sample infinite to complete the following table:
| 10 | P(x) | x P(x) | (x – μ)2 |
|---|---|---|---|
| 0 | | 0 | (0 – 1)2 ⋅ |
| 1 | | | (1 – 1)ii ⋅ |
| 2 | | | (1 – i)2 ⋅ |
Add the values in the third column to observe the expected value: μ = ![]() = 1. Use this value to consummate the quaternary column.
= 1. Use this value to consummate the quaternary column.
Add the values in the quaternary column and take the foursquare root of the sum: σ = ![]() ≈ 0.7071.
≈ 0.7071.
On May eleven, 2013 at 9:30 PM, the probability that moderate seismic activity (one moderate earthquake) would occur in the next 48 hours in Iran was about 21.42%. Suppose y'all make a bet that a moderate earthquake will occur in Iran during this catamenia. If y'all win the bet, you win ?l. If yous lose the bet, you pay ?twenty. Let 10 = the corporeality of profit from a bet.
P(win) = P(1 moderate convulsion will occur) = 21.42%
P(loss) = P(ane moderate earthquake volition not occur) = 100% – 21.42%
If you bet many times, will you come out ahead? Explain your answer in a complete sentence using numbers. What is the standard difference of X? Construct a table similar to (Effigy) and (Effigy) to assistance you answer these questions.
| x | P(x) | 10 (Px) | (ten – μ)2 P(x) | |
|---|---|---|---|---|
| win | 50 | 0.2142 | 10.71 | [50 – (–v.006)]2(0.2142) = 648.0964 |
| loss | –20 | 0.7858 | –15.716 | [–20 – (–five.006)]2(0.7858) = 176.6636 |
Mean = Expected Value = 10.71 + (–fifteen.716) = –five.006.
If you make this bet many times nether the aforementioned conditions, your long term outcome will be an average loss of ?five.01 per bet.
![]()
Attempt It
On May 11, 2013 at 9:30 PM, the probability that moderate seismic activeness (one moderate earthquake) would occur in the next 48 hours in Japan was about 1.08%. As in (Figure), yous bet that a moderate convulsion will occur in Nihon during this catamenia. If you win the bet, you lot win ?100. If you lose the bet, you pay ?x. Allow X = the amount of turn a profit from a bet. Find the mean and standard departure of X.
Some of the more common detached probability functions are binomial, geometric, hypergeometric, and Poisson. Most simple courses do not cover the geometric, hypergeometric, and Poisson. Your instructor will let you lot know if he or she wishes to comprehend these distributions.
A probability distribution function is a design. You try to fit a probability problem into a pattern or distribution in guild to perform the necessary calculations. These distributions are tools to brand solving probability problems easier. Each distribution has its own special characteristics. Learning the characteristics enables you lot to distinguish among the different distributions.
Chapter Review
The expected value, or mean, of a discrete random variable predicts the long-term results of a statistical experiment that has been repeated many times. The standard departure of a probability distribution is used to measure out the variability of possible outcomes.
Formula Review
Hateful or Expected Value: ![]()
Standard Deviation: ![]()
Complete the expected value table.
| ten | P(x) | 10*P(x) |
|---|---|---|
| 0 | 0.2 | |
| 1 | 0.2 | |
| 2 | 0.four | |
| 3 | 0.2 |
<!– <solution id="fs-idm67031296″>
–>
Discover the expected value from the expected value table.
| x | P(x) | x*P(10) |
|---|---|---|
| 2 | 0.1 | ii(0.1) = 0.2 |
| 4 | 0.three | 4(0.3) = 1.2 |
| half dozen | 0.4 | half-dozen(0.4) = two.4 |
| 8 | 0.2 | eight(0.two) = 1.6 |
0.2 + i.2 + ii.4 + 1.6 = 5.4
Observe the standard difference.
| x | P(x) | x*P(ten) | (x – μ)ii P(x) |
|---|---|---|---|
| 2 | 0.ane | 2(0.ane) = 0.2 | (2–5.4)two(0.1) = 1.156 |
| iv | 0.3 | four(0.three) = 1.2 | (iv–5.4)2(0.3) = 0.588 |
| 6 | 0.iv | 6(0.4) = 2.4 | (6–5.4)2(0.4) = 0.144 |
| eight | 0.ii | 8(0.2) = 1.half-dozen | (8–5.4)2(0.2) = 1.352 |
<!– <solution id="fs-idm40043568″> σ= one.156+0.588+0.144+1.352 = three.24 =one.8 –>
Place the error in the probability distribution tabular array.
| x | P(10) | x*P(x) |
|---|---|---|
| i | 0.15 | 0.fifteen |
| 2 | 0.25 | 0.fifty |
| 3 | 0.30 | 0.90 |
| 4 | 0.20 | 0.eighty |
| 5 | 0.fifteen | 0.75 |
The values of P(10) exercise not sum to one.
Identify the mistake in the probability distribution table.
| x | P(x) | x*P(x) |
|---|---|---|
| 1 | 0.fifteen | 0.15 |
| 2 | 0.25 | 0.40 |
| 3 | 0.25 | 0.65 |
| iv | 0.20 | 0.85 |
| v | 0.fifteen | i |
<!– <solution id="fs-idp3065552″> The values of xP(ten) are not right. –>
Use the following information to answer the next five exercises: A physics professor wants to know what per centum of physics majors will spend the next several years doing post-graduate research. He has the following probability distribution.
| 10 | P(x) | ten*P(ten) |
|---|---|---|
| 1 | 0.35 | |
| ii | 0.20 | |
| 3 | 0.15 | |
| 4 | ||
| five | 0.10 | |
| 6 | 0.05 |
Define the random variable X.
Let 10 = the number of years a physics major will spend doing mail-graduate enquiry.
Define P(ten), or the probability of ten.
<!– <solution id="fs-idm55979056″> Allow P(x) = the probability that a physics major will do post-graduate research for 10 years. –>
Observe the probability that a physics major will do post-graduate inquiry for 4 years. P(x = four) = _______
i – 0.35 – 0.xx – 0.15 – 0.x – 0.05 = 0.xv
FInd the probability that a physics major volition do postal service-graduate research for at most 3 years. P(ten ≤ iii) = _______
<!– <solution id="fs-idp5192912″> 0.35 + 0.20 + 0.fifteen = 0.lxx –>
On average, how many years would you expect a physics major to spend doing post-graduate inquiry?
1(0.35) + ii(0.xx) + iii(0.xv) + 4(0.15) + v(0.x) + 6(0.05) = 0.35 + 0.40 + 0.45 + 0.60 + 0.50 + 0.30 = 2.6 years
Employ the post-obit data to answer the side by side seven exercises: A ballet instructor is interested in knowing what pct of each twelvemonth's form will continue on to the next, so that she tin program what classes to offer. Over the years, she has established the following probability distribution.
- Permit X = the number of years a student will study ballet with the teacher.
- Let P(x) = the probability that a student will study ballet x years.
Complete (Figure) using the information provided.
| x | P(x) | x*P(x) |
|---|---|---|
| one | 0.10 | |
| two | 0.05 | |
| iii | 0.10 | |
| 4 | ||
| 5 | 0.30 | |
| 6 | 0.twenty | |
| 7 | 0.x |
In words, define the random variable X.
10 is the number of years a educatee studies ballet with the teacher.
P(x = 4) = _______
<!– <solution id="fs-idp93530752″> one – 0.10 – 0.05 – 0.x – 0.30 – 0.xx – 0.x = 0.15 –>
P(ten < four) = _______
0.10 + 0.05 + 0.ten = 0.25
On average, how many years would you expect a kid to study ballet with this teacher?
<!– <solution id="fs-idp209095920″> 1(0.10) + 2(0.05) + 3(0.10) + iv(0.15) + 5(0.30) + half dozen(0.20) + 7(0.10) = iv.5 years –>
What does the cavalcade "P(x)" sum to and why?
The sum of the probabilities sum to i because it is a probability distribution.
What does the column "ten*P(x)" sum to and why?
<!– <solution id="fs-idp175794960″> The sum of xP(10) = 4.v; it is the hateful of the distribution. –>
Y'all are playing a game by drawing a carte du jour from a standard deck and replacing information technology. If the card is a face carte du jour, you win ?30. If it is not a face carte du jour, you pay ?ii. There are 12 face cards in a deck of 52 cards. What is the expected value of playing the game?
![]()
You are playing a game by drawing a card from a standard deck and replacing it. If the bill of fare is a face card, you win ?xxx. If it is not a face bill of fare, y'all pay ?2. There are 12 face cards in a deck of 52 cards. Should you play the game?
<!– <solution id="fs-idm123320016″> Yes, because there is a positive expected value, and the more yous play, the more probable you are to go closer to the expected value. –>
HOMEWORK
A theater group holds a fund-raiser. Information technology sells 100 raffle tickets for ?five apiece. Suppose you purchase four tickets. The prize is ii passes to a Broadway show, worth a full of ?150.
- What are y'all interested in here?
- In words, define the random variable X.
- List the values that X may take on.
- Construct a PDF.
- If this fund-raiser is repeated often and you e'er buy 4 tickets, what would be your expected average winnings per raffle?
<!– <solution id="fs-idp146807296″> I am interested in the average turn a profit or loss. Let 10 = the return from the raffle Win(💲150) or Lose (💲0)
150( 1 100 )+0( 99 100 )−20=−💲eighteen.50 –>
A game involves selecting a card from a regular 52-card deck and tossing a coin. The coin is a fair coin and is equally likely to land on heads or tails.
- If the carte du jour is a face bill of fare, and the coin lands on Heads, you win ?half dozen
- If the carte is a face card, and the coin lands on Tails, y'all win ?2
- If the card is not a face card, y'all lose ?2, no affair what the coin shows.
- Find the expected value for this game (expected net proceeds or loss).
- Explain what your calculations indicate most your long-term average profits and losses on this game.
- Should yous play this game to win coin?
The variable of interest is X, or the gain or loss, in dollars.
The face cards jack, queen, and king. In that location are (iii)(iv) = 12 face cards and 52 – 12 = 40 cards that are not face cards.
We first demand to construct the probability distribution for X. Nosotros utilise the bill of fare and coin events to determine the probability for each consequence, but we use the monetary value of 10 to make up one's mind the expected value.
| Card Consequence | X net proceeds/loss | P(X) |
|---|---|---|
| Face up Carte and Heads | 6 | |
| Face Card and Tails | 2 | |
| (Not Face Menu) and (H or T) | –2 | |
-
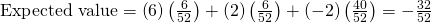
- Expected value = –?0.62, rounded to the nearest cent
- If you lot play this game repeatedly, over a long cord of games, you would expect to lose 62 cents per game, on average.
- You lot should not play this game to win money because the expected value indicates an expected average loss.
Yous buy a lottery ticket to a lottery that costs ?10 per ticket. There are but 100 tickets available to be sold in this lottery. In this lottery at that place are 1 ?500 prize, two ?100 prizes, and four ?25 prizes. Find your expected gain or loss.
<!– <solution id="eip-id1170585488797″> Beginning by writing the probability distribution. 10 is net proceeds or loss = prize (if whatever) less 💲x cost of ticket
Expected Value =(490)( 1 100 )+(ninety)( 2 100 )+(15)( 4 100 )+(−10)( 93 100 )=−💲2. There is an expected loss of 💲2 per ticket, on average. –>
Complete the PDF and answer the questions.
| x | P(x) | ten P(ten) |
|---|---|---|
| 0 | 0.iii | |
| 1 | 0.2 | |
| 2 | ||
| iii | 0.4 |
- Discover the probability that x = 2.
- Observe the expected value.
- 0.1
- one.6
Suppose that yous are offered the post-obit "deal." You curlicue a die. If yous roll a six, yous win ?ten. If you roll a iv or five, you win ?5. If you roll a ane, 2, or 3, y'all pay ?vi.
- What are you ultimately interested in here (the value of the roll or the coin you win)?
- In words, ascertain the Random Variable X.
- List the values that Ten may accept on.
- Construct a PDF.
- Over the long run of playing this game, what are your expected boilerplate winnings per game?
- Based on numerical values, should you take the bargain? Explicate your determination in consummate sentences.
<!– <solution id="fs-idp133159792″> the coin won X = the amount of money won or lost 💲5, –💲6, 💲10
Expected Value = (ten) 1 half-dozen + (v) two 6 – (half dozen) 3 6 = 0.33 Yes, the expected value is 33 cents –>
A venture capitalist, willing to invest ?ane,000,000, has three investments to choose from. The first investment, a software company, has a 10% gamble of returning ?v,000,000 profit, a 30% take chances of returning ?1,000,000 profit, and a 60% chance of losing the meg dollars. The second visitor, a hardware company, has a 20% run a risk of returning ?3,000,000 profit, a 40% chance of returning ?1,000,000 profit, and a 40% run a risk of losing the million dollars. The third visitor, a biotech business firm, has a ten% chance of returning ?6,000,000 profit, a 70% of no profit or loss, and a 20% gamble of losing the million dollars.
- Construct a PDF for each investment.
- Detect the expected value for each investment.
- Which is the safest investment? Why do you call up so?
- Which is the riskiest investment? Why do yous think and then?
- Which investment has the highest expected render, on average?
-
Software Company x P(x) v,000,000 0.ten ane,000,000 0.30 –1,000,000 0.60 Hardware Company x P(x) 3,000,000 0.twenty 1,000,000 0.40 –1,000,00 0.40 Biotech Firm ten P(10) 6,00,000 0.10 0 0.70 –ane,000,000 0.twenty - ?200,000; ?600,000; ?400,000
- third investment because information technology has the everyman probability of loss
- first investment because it has the highest probability of loss
- second investment
Suppose that twenty,000 married adults in the United States were randomly surveyed every bit to the number of children they have. The results are compiled and are used as theoretical probabilities. Let 10 = the number of children married people take.
| ten | P(ten) | x P(10) |
|---|---|---|
| 0 | 0.10 | |
| 1 | 0.20 | |
| 2 | 0.xxx | |
| 3 | ||
| 4 | 0.x | |
| 5 | 0.05 | |
| half dozen (or more than) | 0.05 |
- Find the probability that a married adult has three children.
- In words, what does the expected value in this example correspond?
- Detect the expected value.
- Is it more likely that a married developed volition have two to three children or four to six children? How do you know?
<!– <solution id="eip-idp44220400″> 0.ii The average number of children married adults have. 2.35 two of three children –>
Suppose that the PDF for the number of years it takes to earn a Bachelor of Scientific discipline (B.South.) degree is given as in (Effigy).
| x | P(x) |
|---|---|
| 3 | 0.05 |
| four | 0.forty |
| v | 0.30 |
| half-dozen | 0.xv |
| vii | 0.10 |
On boilerplate, how many years do you expect it to take for an individual to earn a B.S.?
4.85 years
People visiting video rental stores ofttimes rent more than one DVD at a time. The probability distribution for DVD rentals per customer at Video To Go is given in the following table. There is a five-video limit per customer at this shop, so nobody ever rents more than five DVDs.
| x | P(x) |
|---|---|
| 0 | 0.03 |
| i | 0.50 |
| ii | 0.24 |
| 3 | |
| iv | 0.07 |
| 5 | 0.04 |
- Describe the random variable Ten in words.
- Find the probability that a customer rents three DVDs.
- Observe the probability that a customer rents at least four DVDs.
- Find the probability that a customer rents at nearly 2 DVDs.
Another shop, Entertainment Headquarters, rents DVDs and video games. The probability distribution for DVD rentals per client at this shop is given as follows. They also have a five-DVD limit per customer.
x P(x) 0 0.35 1 0.25 2 0.xx 3 0.10 four 0.05 v 0.05 - At which store is the expected number of DVDs rented per client higher?
- If Video to Go estimates that they will have 300 customers side by side week, how many DVDs do they wait to rent next week? Respond in sentence form.
- If Video to Go expects 300 customers adjacent week, and Entertainment HQ projects that they will have 420 customers, for which shop is the expected number of DVD rentals for adjacent week higher? Explain.
- Which of the two video stores experiences more than variation in the number of DVD rentals per customer? How practice you know that?
<!– <solution id="fs-idp138954192″> X = the number of video rentals per costumer 0.12 0.xi 0.77 Video To Go (ane.82 expected value vs. i.4 for Entertainment Headquarters) The expected number of videos rented to 300 Video To Go customers is 546. The expected number of videos rented to 420 Amusement Headquarters customers is 588. Entertainment Headquarters will hire more than videos. The standard departure for the number of videos rented at Video To Get is i.1609. The standard deviation for the number of videos rented at Entertainment Headquarters is one.4293. Entertainment Headquarters has more variation. –>
<!–Review Questions??–>
A "friend" offers you the following "deal." For a ?10 fee, y'all may pick an envelope from a box containing 100 seemingly identical envelopes. However, each envelope contains a coupon for a gratis souvenir.
- Ten of the coupons are for a free souvenir worth ?6.
- Eighty of the coupons are for a complimentary gift worth ?8.
- Six of the coupons are for a free gift worth ?12.
- Iv of the coupons are for a free gift worth ?40.
Based upon the financial gain or loss over the long run, should you play the game?
- Yes, I wait to come out ahead in money.
- No, I expect to come out behind in money.
- It doesn't matter. I expect to break even.
b
Florida State Academy has fourteen statistics classes scheduled for its Summer 2013 term. One form has space available for thirty students, viii classes have space for 60 students, one class has space for 70 students, and four classes take space for 100 students.
- What is the average grade size assuming each class is filled to capacity?
- Space is available for 980 students. Suppose that each class is filled to chapters and select a statistics student at random. Let the random variable Ten equal the size of the student's class. Define the PDF for X.
- Find the hateful of X.
- Find the standard deviation of 10.
<!– <solution id="fs-idm42546736″> The average class size is: 30+viii(60)+lxx+four(100) fourteen =70 P(x=30)= 1 14 P(10=60)= eight 14 P(10=70)= 1 14 P(10=100)= 4 xiv Complete the following table to detect the mean and standard deviation of 10.
Hateful of X= xxx 14 + 480 14 + lxx 14 + 400 14 = 980 14 =seventy Standard Deviation of 10= 114.2857+57.1429+0+257.1429 =xx.702 –>
In a lottery, at that place are 250 prizes of ?v, fifty prizes of ?25, and ten prizes of ?100. Assuming that 10,000 tickets are to be issued and sold, what is a fair price to charge to break even?
Let X = the amount of money to be won on a ticket. The post-obit table shows the PDF for X.
| x | P(x) |
|---|---|
| 0 | 0.969 |
| 5 | |
| 25 | |
| 100 | |
Calculate the expected value of X.
0(0.969) + 5(0.025) + 25(0.005) + 100(0.001) = 0.35
A off-white cost for a ticket is ?0.35. Any cost over ?0.35 will enable the lottery to raise money.
Source: https://opentextbc.ca/introstatopenstax/chapter/mean-or-expected-value-and-standard-deviation/
Posted by: fullerondowde.blogspot.com


0 Response to "How To Find The Expected Value Of A Probability Distribution"
Post a Comment