How To Find The X Coordinate Of The Vertex

Hotmath

• Dwelling

The Vertex of a Parabola

The vertex of a parabola is the point where the parabola crosses its axis of symmetry.   If the coefficient of the ${\mathrm{ten}}^{\mathrm{ii}}$ term is positive, the vertex will be the lowest bespeak on the graph, the point at the lesser of the " $U$ "-shape.  If the coefficient of the $x^2$ term is negative, the vertex will be the highest indicate on the graph, the betoken at the top of the " $U$ "-shape.

The standard equation of a parabola is

$y=a{x}^2+b\mathrm{10}+c$ .

But the equation for a parabola can too be written in "vertex form":

$y=a{(x-h)}^{\mathrm{ii}}+g$

In this equation, the vertex of the parabola is the point $(h,k)$ .

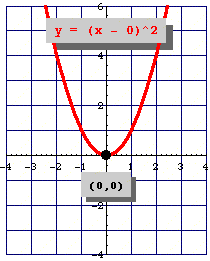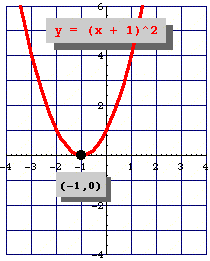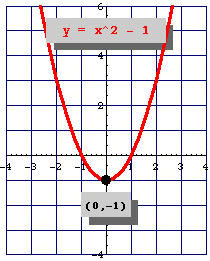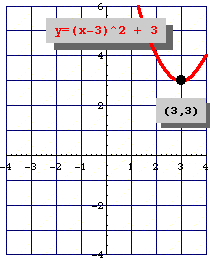
You can see how this relates to the standard equation by multiplying it out:

$\begin{array}{l}y=a(x-h)(x-h)+\mathrm{chiliad}\\ y=a{\mathrm{10}}^2-\mathrm{two}ahx+a{h}^2+k\end{array}$ .

This ways that in the standard form, $y=a{x}^2+bx+c$ , the expression $-\frac{b}{2a}$ gives the $x$ -coordinate of the vertex.

Example:

Find the vertex of the parabola.

$y=3x^2+12\mathrm{ten}-12$

Here, $a=3$ and $b=12$ . So, the $x$ -coordinate of the vertex is:

$-\frac{12}{2\left(3\right)}=-\mathrm{ii}$

Substituting in the original equation to get the $y$ -coordinate, we get:

$\begin{array}{l}y=\mathrm{three}{\left(-2\right)}^{\mathrm{two}}+12\left(-\mathrm{ii}\right)-12\\ =-24\end{array}$

So, the vertex of the parabola is at $(-2,-24)$ .

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/vertex-of-a-parabola

Posted by: fullerondowde.blogspot.com

Share this post