How To Find Slope With One Point
How practice we find the gradient of a linear equation? Allow'due south dive in and detect!

While mathematics is oft grouped with the sciences, in some respects, math is a beautiful language. For instance, when comparison how something grows, one might say information technology grows slowly, moderately, or apace. Merely, how slowly? How quickly? Using mathematics, nosotros can depict the growth of functions using slope.
In this review, we will explain how to find slope, focusing on linear functions. By the finish, y'all will know how to find the slope of a line. This includes how to find slope with two points, how to find slope using a graph, and how to find the gradient of an equation.
What is slope?
Gradient describes the rate of change or "steepness" of a line.
A linear function will look like a straight line when graphed. Here are some examples of linear equations and their slopes (click images to expand):
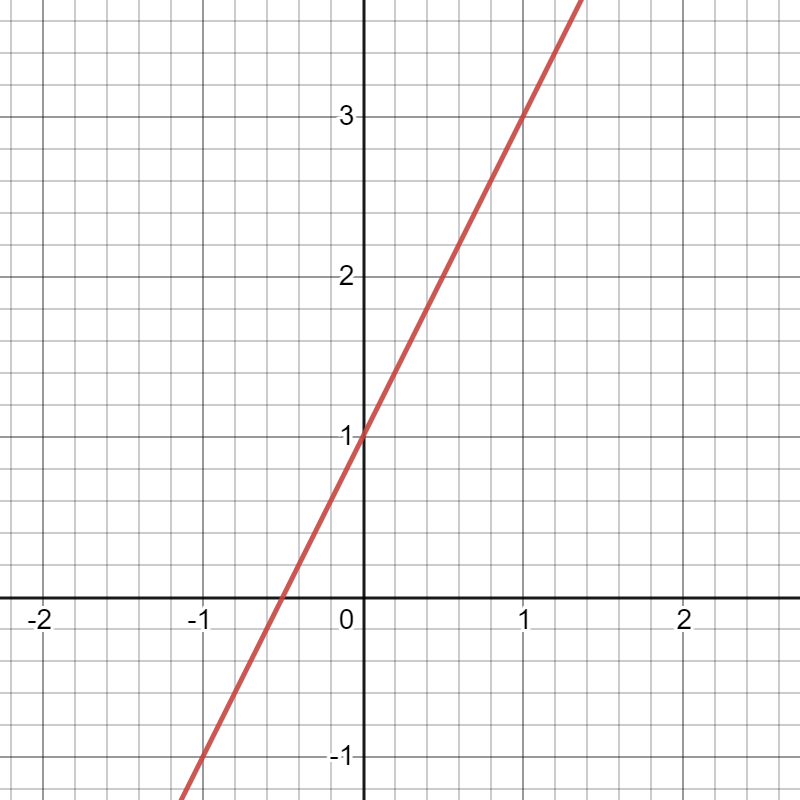
Slope: 2
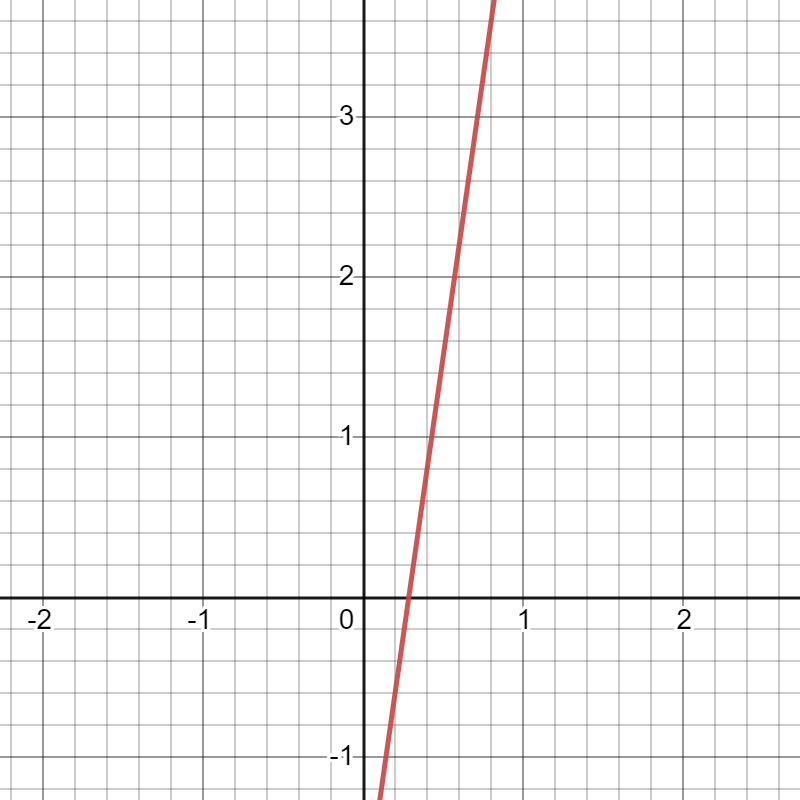
Slope: 7
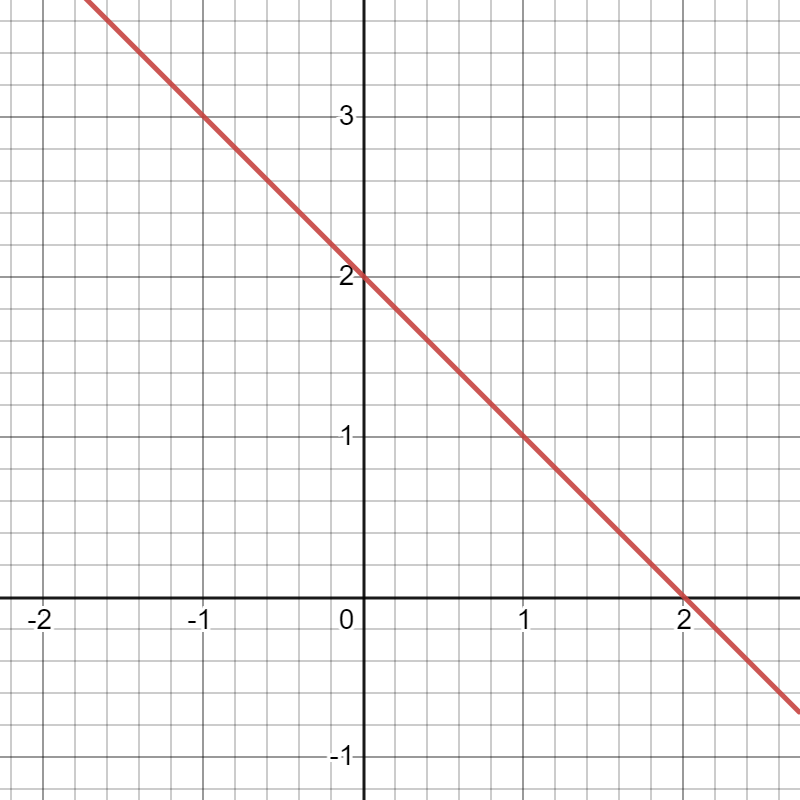
Slope: -1
What is the formula for slope?
For two points with the coordinate (x_1, y_1) and (x_2, y_2), the formula for slope is:
yard=\dfrac{y_2-y_1}{x_2-x_1}
"Rise Over Run"
The slope of a line can be described every bit rise over run .
The rise is the vertical change in y and the run is the horizontal change in ten.
In the gradient formula above, the letter of the alphabet yard represents the gradient.
Beneath is a visual to sympathize what we hateful by "rise" (vertical alter shown in the dotted blue line) and "run" (horizontal alter shown in the dotted green line):

Negative vs Positive Slope of Linear Equations
Positive Slope
When a function has a positive slope, the line is moving upwards from left to right. In other words, every bit the value of ten increases, the value of y also increases. The greater the slope of a positive-slope line, the steeper the line is.
For example, a slope of vii would create a steeper line than a gradient of ii.
Here are some examples of lines with positive slopes (click images to aggrandize):
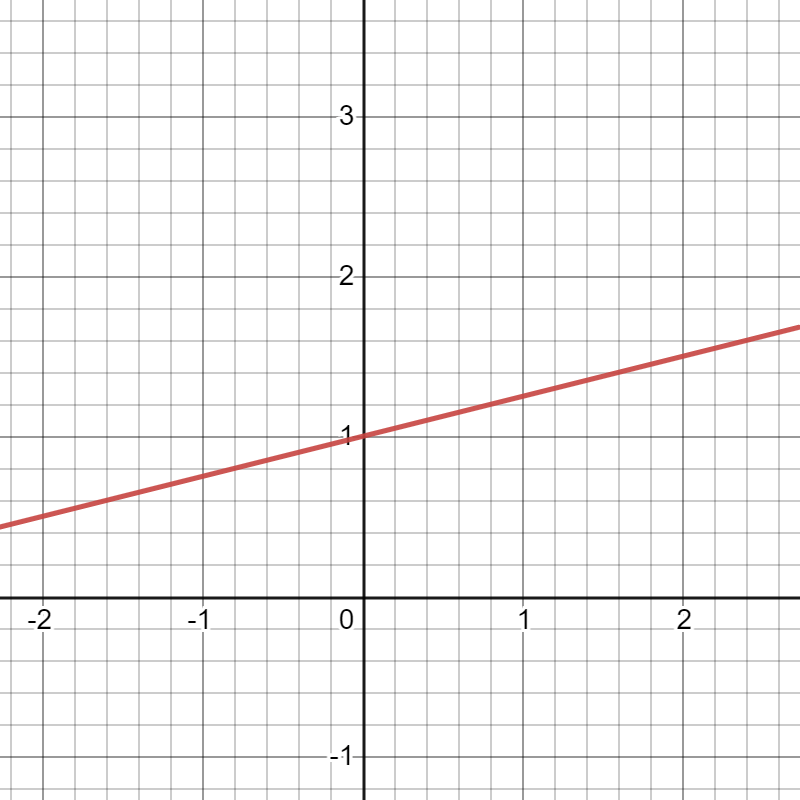
Gradient: \frac{ 1}{4 }
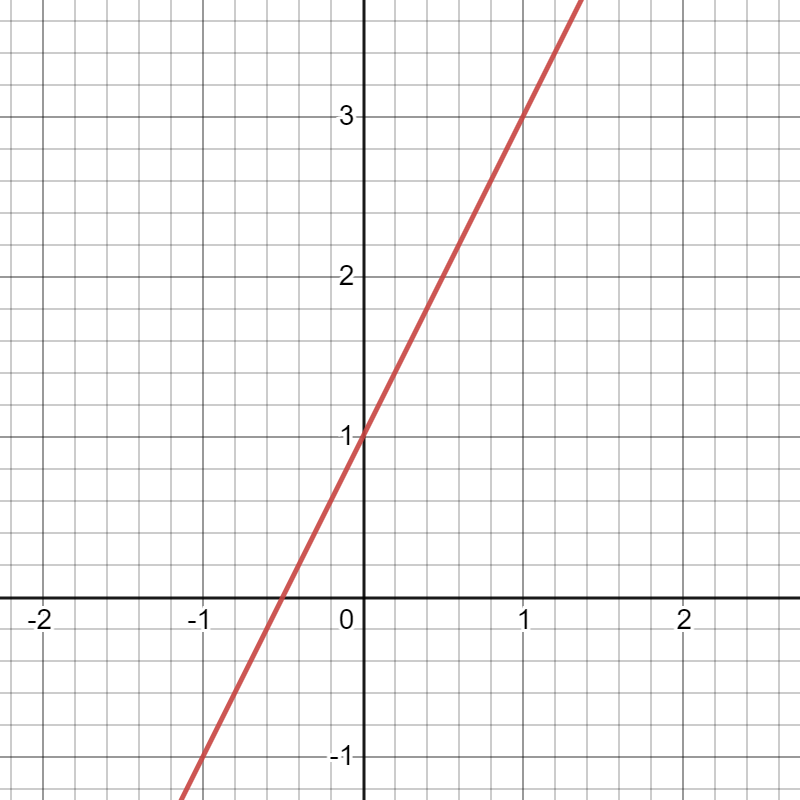
Slope: 2
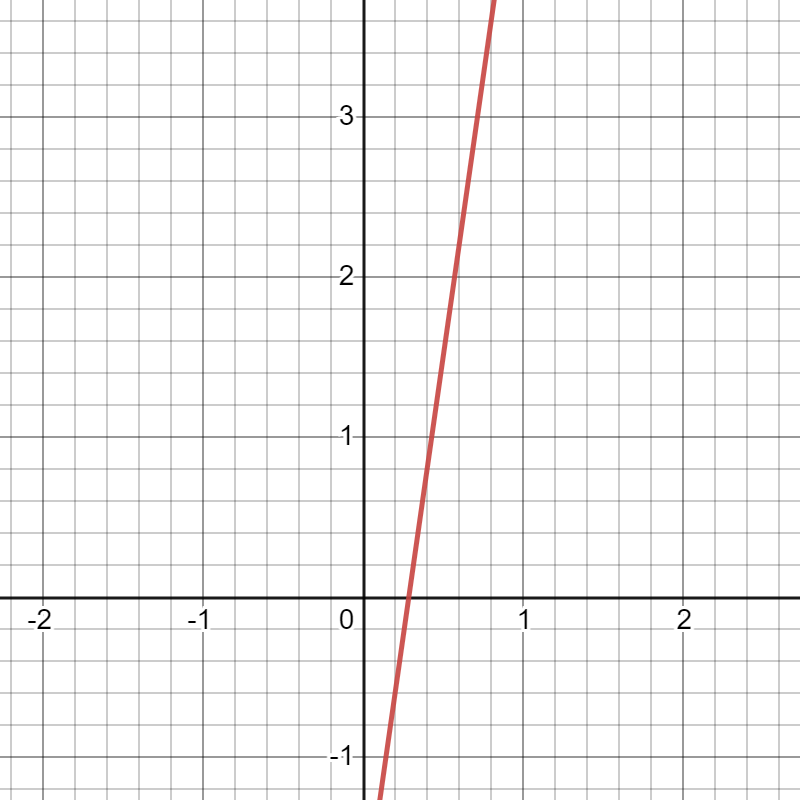
Slope: 7
Negative Slope
When a function has a negative slope, the line is moving down from left to right. In other words, as the value of ten increases, the value of y decreases. The lower the gradient of a negative-slope line, the steeper the line is.
For example, a slope of -10 would create a steeper line than a gradient of -2.
Hither are some examples of lines with negative slopes (click images to expand):
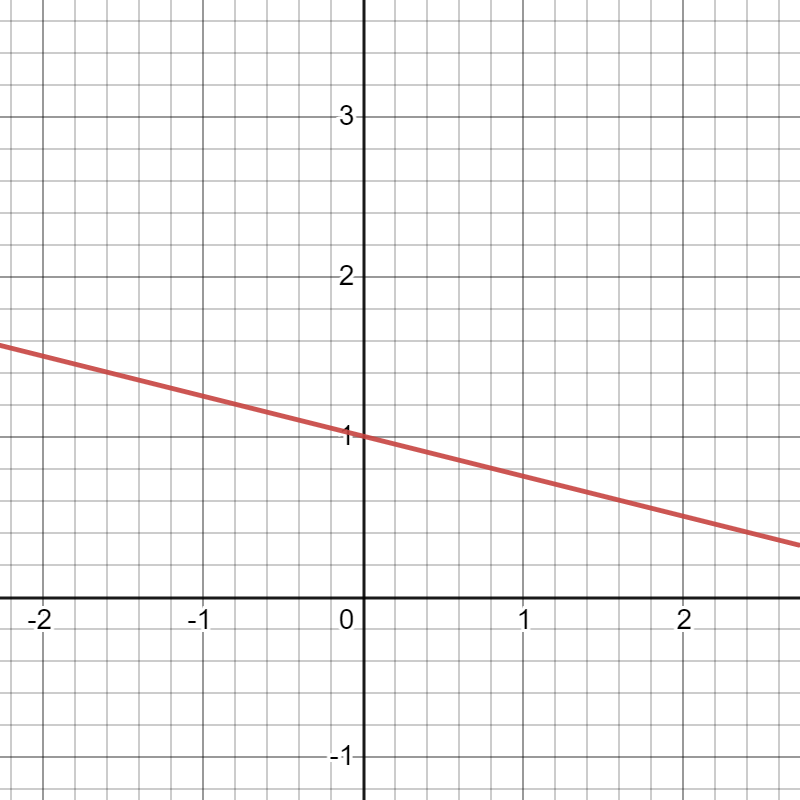
Slope: - \frac{ i}{iv }
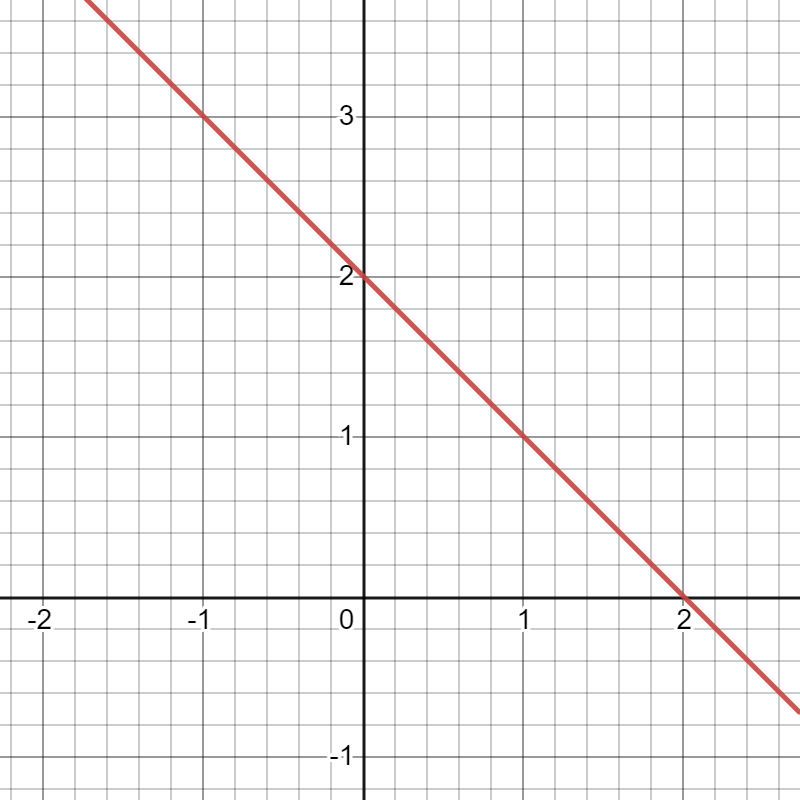
Slope: -1
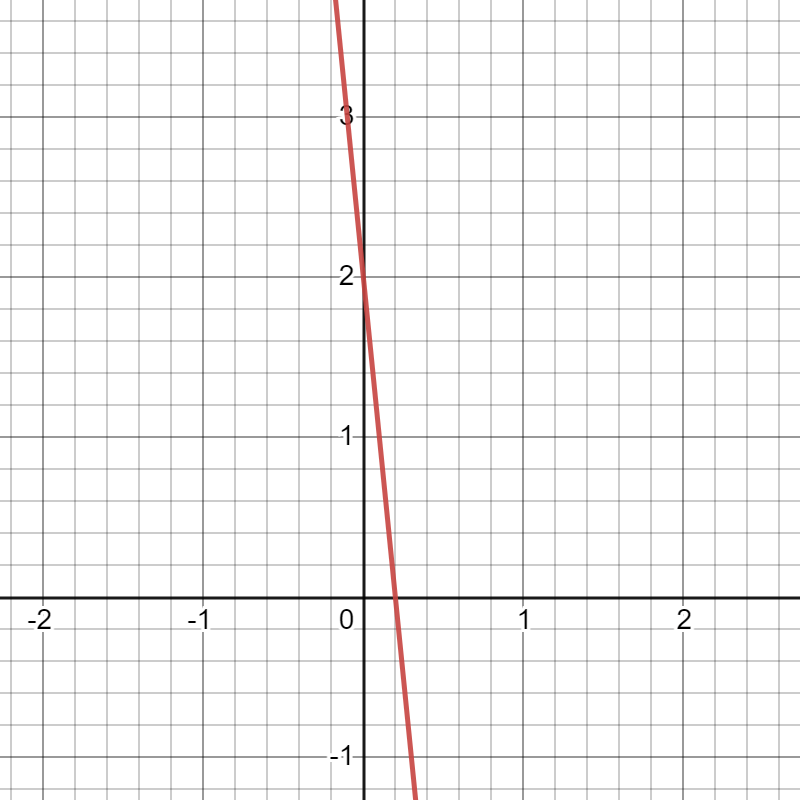
Slope: -10
Find Slope from Two Points (Instance)
We volition now talk about how to find gradient with two points.
Let's brainstorm with a simple instance. We volition use Point A, (5,8) and Betoken B (1,4) .
Retrieve, we can outset with the formula for slope:
m=\dfrac{y_2-y_1}{x_2-x_1}
Before we can substitute the values into the equation, we should label the points.


Now, nosotros tin can substitute v for x_1, viii for y_1, 1 for x_2 and 4 for y_2.
\dfrac{y_2-y_1}{x_2-x_1}
\dfrac{4-8}{one-5}
And next, we simplify to observe the slope of the line.
\dfrac{-4}{-four} = 1
Therefore, the slope of a line going through Bespeak A, (v,8) and Point B (one,4) would exist 1. That was an example of how to find the slope when given 2 points.
If helpful, here's a quick video explaining how to calculate the slope when given ii points:
Find Slope From a Graph (Instance)
To calculate the gradient of a line from a graph, nosotros employ the graph to decide the rise (the vertical change) and the run (the horizontal change)
To begin, nosotros select two points on the graph that are easy to identify. Nosotros tin can consider the line y=2x-1 equally an example.
On the graph shown beneath, the ruby-red line represents y=2x-ane. Nosotros can identify the points (1,1) and (2,3) on this line.
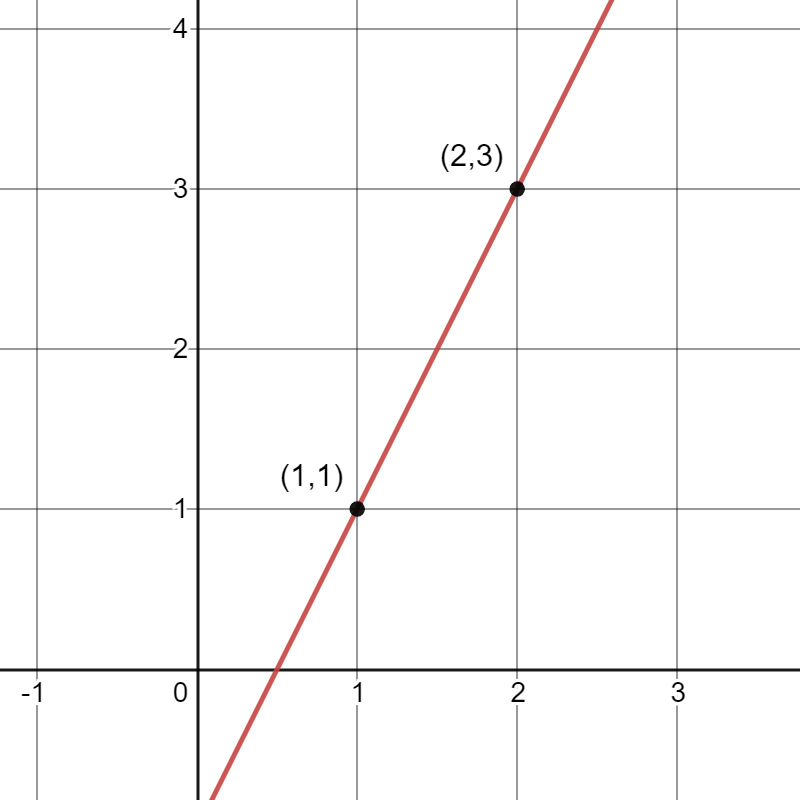
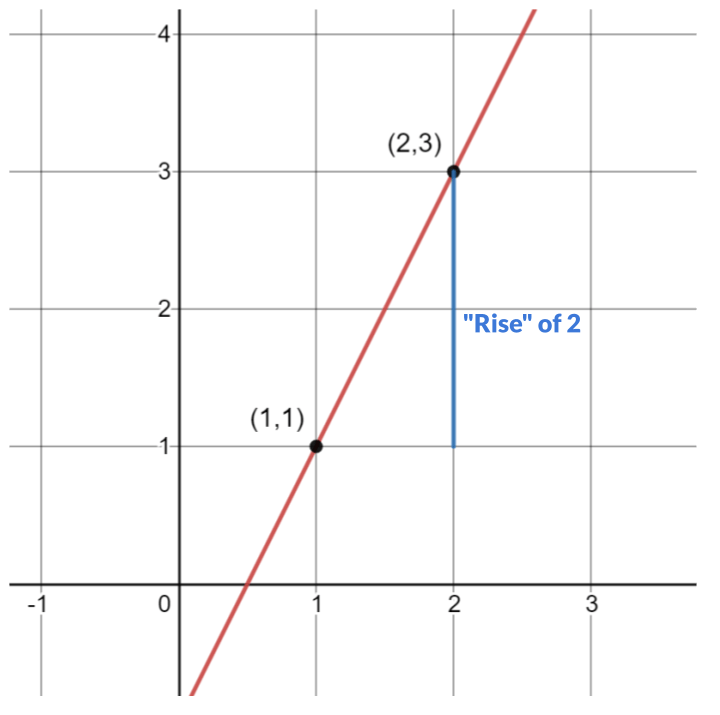
Now, we can count the vertical distance betwixt the points to determine the rise. In the following image, the vertical distance of {2} is in blue, shown below:
We besides must count the horizontal distance between the points to determine the run. In the following image, the horizontal distance of {i} is in light-green.
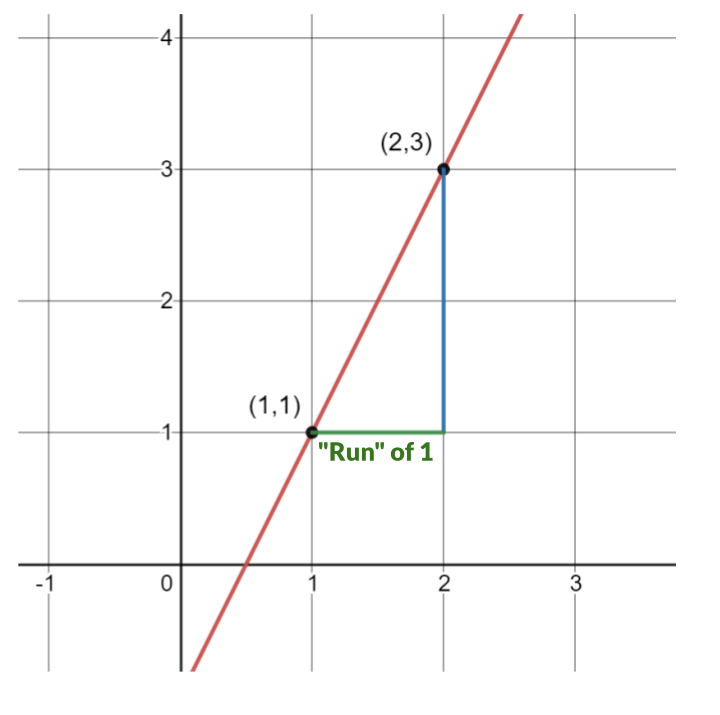
Therefore, the rise is {2} and the run is {1} . The slope is ascension over run or \dfrac{2}{1} which simplifies to 2.
We now know how to find slope using a graph!
For those who prefer videos, here's a quick clip showing this method of finding slope from a graph:
Find Slope From an Equation (Example)
If you want to know how to discover the slope of a linear equation, you lot must first know that linear equations are frequently written in slope-intercept class.
In slope-intercept course, an equation is written:
y=mx+b
The letter m represents the slope and the alphabetic character b represents the y-intercept.
To determine how to find slope, you must identify the coefficient in front of x.
For example, consider the equation:
y=7x+10
The coefficient in front of ten is 7. Therefore, we know the slope of the line y=7x+ten is 7.
If you encounter an equation in a different form, simply solve the equation for y and write the equation in slope-intercept form. And so, y'all can utilize this method to determine the slope.
In addition, this article has some great real-life applications of slope.
And here's a quick video on how to observe the slope of a line when given an equation:
Slope of Horizontal and Vertical Lines
When learning how to calculate slope, there are 2 unusual cases that require some special attention: horizontal and vertical lines.
Horizontal Lines
If you lot are finding gradient from two points and you end up with zero in the numerator, you have found the slope of a horizontal line.
This slope of a horizontal line is always 0. The equation of a horizontal line is y=a where a is a real number. Here are two examples of horizontal lines shown in red (click images to expand):
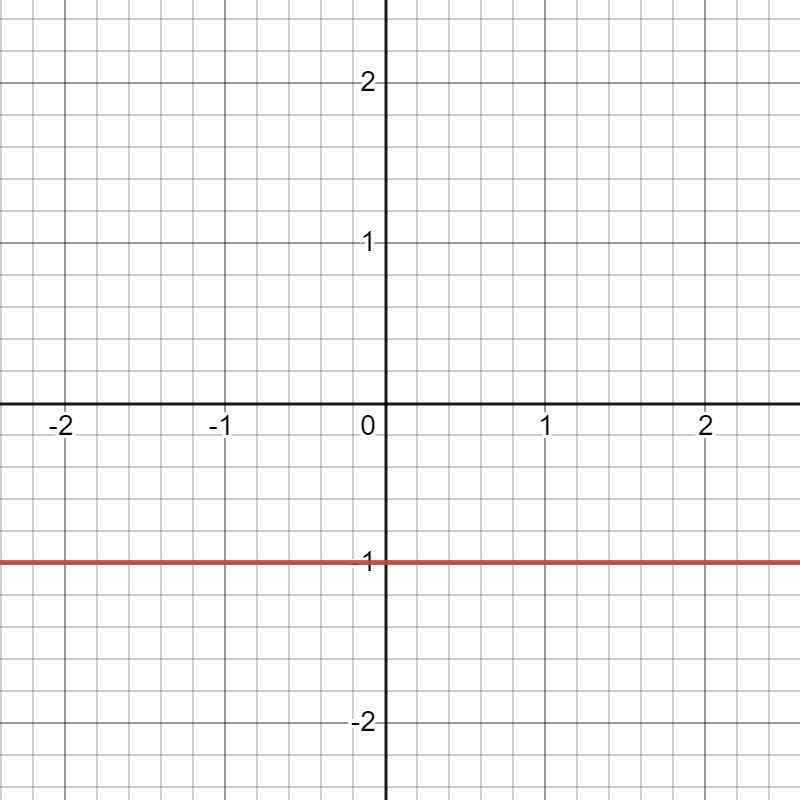
Slope: 0
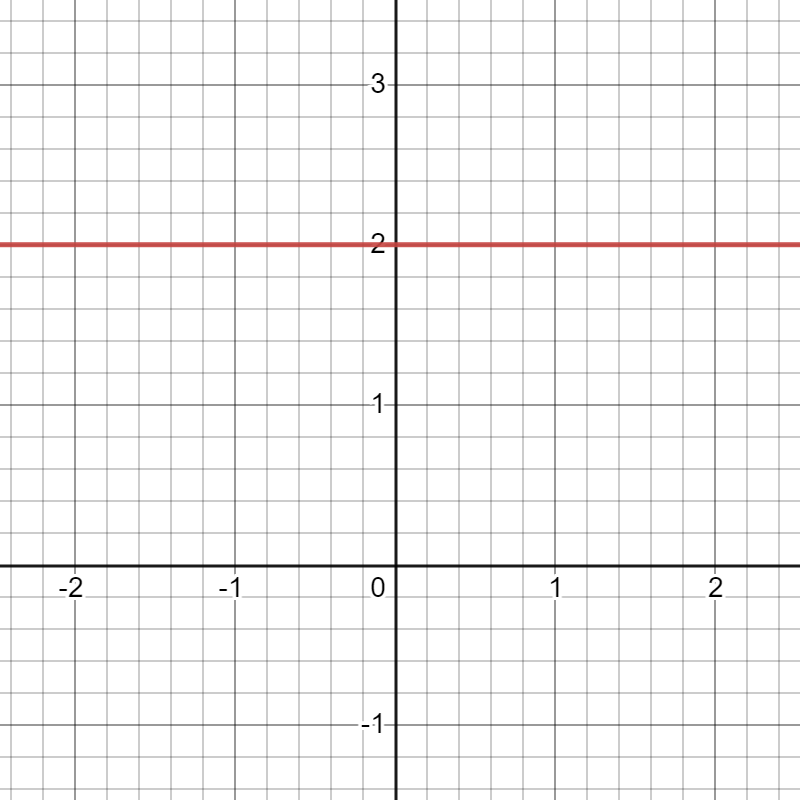
Gradient: 0
Vertical Lines
If you are finding gradient from two points and you cease upwardly with cypher in the denominator, you have institute the slope of a vertical line.
This slope of a vertical line is always undefined.
The equation of a vertical line is x=a where a is a existent number. Here are two examples of vertical lines shown in red (click images to aggrandize):
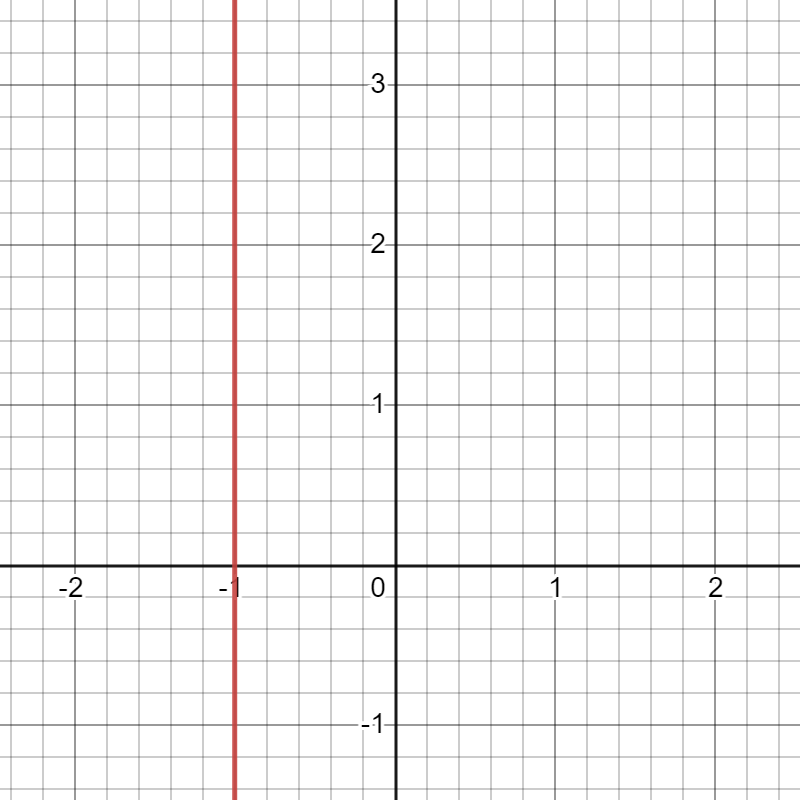
Gradient: undefined
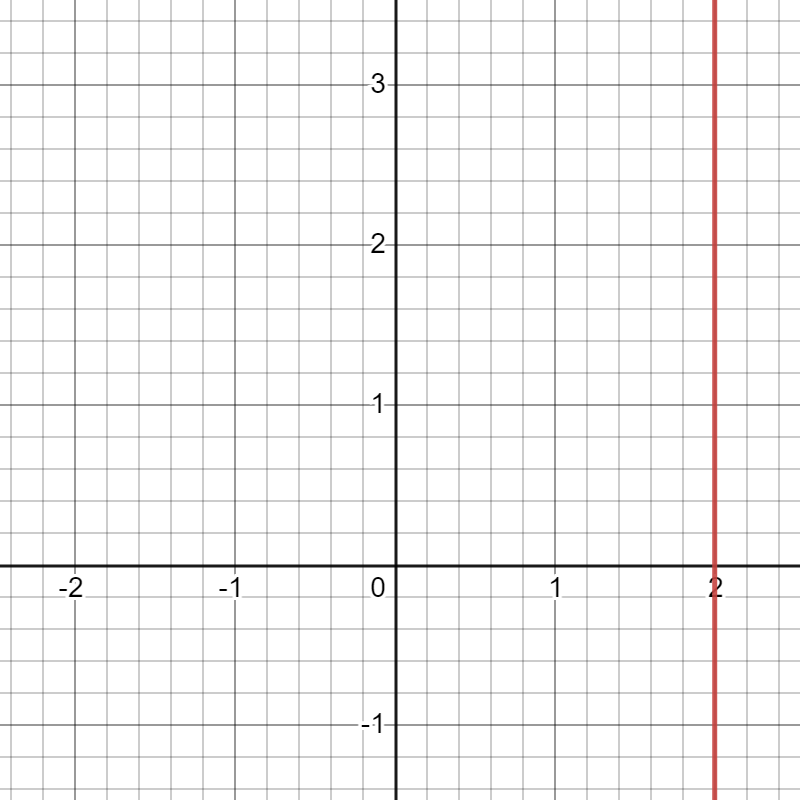
Slope: undefined
Summary: Slope of Linear Equations
- Understanding how to detect gradient can help explain the world around u.s.a.!
- The slope of a linear equation is the "rising over run", or the change in y over the change in x.
- The equation to observe the gradient of a line is:
grand=\dfrac{y_2-y_1}{x_2-x_1}
- Horizontal lines always have a slope of zero and vertical lines always accept an undefined slope.
Practice Problems With Slope
At present that we know how to observe slope with two points, how to detect slope using a graph, and how to find the gradient of an equation, information technology's fourth dimension to exercise our new skills.
In addition, you can explore more of our free detailed review guides of important Algebra 1 topics.
Source: https://www.albert.io/blog/how-to-find-slope/
Posted by: fullerondowde.blogspot.com


0 Response to "How To Find Slope With One Point"
Post a Comment