How To Find The Speed Of An Object
Dispatch is an important concept in physics used to describe motion and solve bug. In this article, we will define acceleration, the formula for acceleration, and its units. We will review examples of how to find acceleration including positive acceleration and negative acceleration.
Review: Kinematic Terms
In that location are a few kinematic terms that you'll need to know to empathise acceleration. The first kinematic term is velocity. Velocity is the rate of alter of position, or the displacement, over fourth dimension. Deportation is another proper noun for the change in position. Remember that an object moving at a constant velocity has a constant change of position every 2d. The motion map below shows an object moving with a constant velocity.
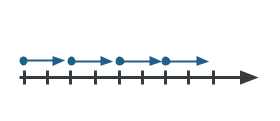
It is as well important to remember the definition of vector quantities. Vectors are quantities that have both a magnitude, or size, and direction. For example, velocity is a vector quantity because it describes both how fast an object is moving (magnitude) and the direction the object is moving in. For an in-depth review of vectors, scalars, displacement, and velocity, visit our Albert blog post introducing kinematics.
What is Acceleration?
Dispatch is defined as the rate of change of velocity. This means that if an object's velocity is increasing or decreasing, so the object is accelerating. Different an object moving at a abiding velocity, an accelerating object will not have a constant change in position every second. An accelerating object could cover more and more distance with every second, or less and less distance every 2d. The beginning motion map beneath shows an accelerating object that is speeding upwards and the 2nd motion map shows an accelerating object that is slowing down.
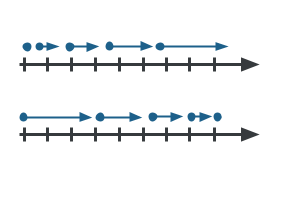
Since acceleration depends on the modify in velocity, dispatch is a vector quantity. This ways that acceleration has both magnitude and management.
The standard units of dispatch are meters per 2nd squared, \text{m/s}^2. These units come from the units of velocity, meters per 2nd, and the units of time, seconds. Since acceleration is the alter in velocity over time, its units are the units of velocity (meters per second) divided past the units of time (second).
For more than data about acceleration and some examples, watch this quick video.
Dispatch Formula
Using our definition of what acceleration is, nosotros can put together a formula for calculating acceleration.
Acceleration Formula
a=\dfrac{\Delta v}{t}
Here, a is acceleration, \Delta v is the change in velocity, and t is time.
Before calculating dispatch, you will often need to start summate the modify in velocity. This is the difference between the object's final velocity, v_f, and its initial velocity, v_i.
Alter in Velocity Formula
\Delta v = v_f - v_i
How to Detect Dispatch
In this next department, we will go over some examples of computing dispatch. Kickoff, we will see an example of positive acceleration, and then an example of negative acceleration.
Example 1: How to Observe the Acceleration of a Car Speeding Upwardly
A automobile starts from rest and moves forward while speeding upwardly to 26\text{ grand/southward} in eight\text{ s}. Calculate the auto'due south acceleration.
The first pace in solving this problem is to determine the change in velocity. Since the automobile started from residue, its initial velocity, v_i, is 0\text{ k/due south}. Its last velocity is 26\text{ m/s}. Therefore, the car'south change in velocity is:
\Delta v = v_f - v_i = 26\text{ m/s} - 0\text{ m/s} = 26\text{ k/s}
Now we tin can calculate the car'southward acceleration by dividing this change in velocity by the time of eight\text{ southward}:
a=\dfrac{\Delta five}{t}
a=\dfrac{26\text{ thou/s}}{8\text{ s}}
a=iii.25\text{ yard/south}^2
Example 2: How to Find the Acceleration of a Car Slowing Down
At present let's consider a state of affairs where an object is slowing downwards.

A motorcar initially moving forward at a velocity of 26\text{ g/s} approaches a schoolhouse and slows down to a velocity of eleven\text{ thousand/s} in 3\text{ due south}. Calculate the car'southward acceleration.
The beginning footstep is to observe the change in velocity. The automobile's initial velocity is 26\text{ m/s} and its final velocity is xi\text{ k/s}. Therefore, the automobile's change in velocity is:
\Delta v = v_f - v_i = 11\text{ chiliad/s} - 26\text{ m/south} = -15\text{ 1000/s}
Now nosotros tin calculate the car'due south acceleration by dividing this change in velocity by the time of 3\text{ south}:
a=\dfrac{\Delta 5}{t}
a=\dfrac{-fifteen\text{ grand/s}}{3\text{ s}}
a=-v\text{ thousand/south}^2
Nosotros will explain in the adjacent section more about what a negative dispatch ways.
Determining the Management of Acceleration
Every bit a vector quantity, acceleration has both magnitude and direction. The direction of dispatch depends on if the object is speeding upwards or slowing down, and the direction the object is moving. In general, if an object is speeding upward, its acceleration volition be in the same direction as its motion. If an object is slowing down, its dispatch is in the opposite management of its motion.
Examples of Positive Acceleration
In that location are two types of situations where an object can have a positive dispatch. If an object is speeding up and moving in a positive direction, it has a positive dispatch. The car speeding up in the get-go case was an example of positive acceleration. The auto is moving forrad in a positive direction and speeding up, so the acceleration is in the same direction as the automobile'southward motion.
An object can also have a positive acceleration if it is slowing downwardly while moving in a negative direction. Since the object is slowing down, the acceleration is in the opposite direction of its move.
Examples of Negative Acceleration
As we saw in the second case, an object tin can take a negative acceleration when the object is slowing downwards while moving in a positive direction. The motorcar in the school zone was moving forwards in a positive direction and slowing downwardly, so the acceleration was in the opposite direction of the motorcar'south movement.
An object can also have a negative acceleration if it is speeding upward while moving in a negative direction. Since the object is speeding up, its acceleration is in the same direction equally its motion.
Using the Acceleration Formula
Now that we have reviewed dispatch and how to discover both its magnitude and direction, nosotros tin apply this knowledge to solve more complicated physics discussion problems.
Instance 1: How to Find Acceleration of a Falling Ball
A ball dropped from residuum reaches a downward velocity of 24.5\text{ grand/s} after falling for 2.5\text{ s}. What is the magnitude and direction of the ball'south acceleration?
To observe the magnitude of the dispatch, we will substitute the given values into the formula for acceleration. Since the ball starts from rest, its initial velocity, v_i is 0\text{ grand/south}.
a=\dfrac{\Delta five}{t}=\dfrac{v_f - v_i}{t}
a=\frac{24.5\text{ thou/south}-0\text{ thousand/s}}{two.5\text{ s}}
a=9.viii\text{ m/s}^ii
Since the brawl is speeding up, the acceleration will exist in the aforementioned direction every bit the ball's motion. The brawl is moving downward in a negative direction. Therefore the direction of the acceleration is also downwards or negative. This tin can be expressed as either -9.8\text{ m/s}^2 or 9.viii\text{ m/s}^ii downward.
Example 2: How to Find Last Velocity of a Skateboarder

A skateboarder with an initial speed of 2\text{ yard/s} accelerates downward a ramp at a rate of 6\text{ m/s}^ii for one.5\text{ s}. What is the skateboarder'south terminal velocity?
The commencement stride to solve this problem is to use the formula for acceleration to make up one's mind the skateboarder's change in velocity. Let'southward substitute the values for acceleration and time into the formula:
a=\dfrac{\Delta five}{t}
vi\text{ m/s}^2=\dfrac{\Delta 5}{one.5\text{ s}}
Now, nosotros can multiply both sides by the fourth dimension to solve for the change in velocity:
\Delta v=(6\text{ m/southward}^2)(1.5\text{ s})=9\text{ g/s}
Change in velocity is the difference between the object's final and initial velocities. Using our change in velocity and the skateboarder's initial velocity produces:
\Delta v = v_f - v_i
9\text{ m/s}=v_f-(2\text{ thousand/southward})
The terminal pace to solve for the final velocity is to add together the initial velocity to the change in velocity:
v_f=9\text{ m/south}+2\text{ m/south}=11\text{ grand/s}
Therefore, the skateboarder'south final velocity is 11\text{ m/due south} directed down the ramp.
Kinematic Equations
Now that y'all know all four kinematic terms (time, displacement, velocity, and acceleration), you will be able to more completely describe the motion of objects. For objects with uniform acceleration, the relationships between these variables are expressed through kinematic equations.
v_f=v_i+at
d=v_i t+\frac{1}{2}at^ii
v_f^ii=v_i^2+2ad
d = \dfrac{v_i + v_f}{2}\cdot t
The kickoff kinematic equation is actually just a variation of the formula for dispatch solved for the terminal velocity. These equations volition permit you to predict the motion of objects and solve for unknown variables in physics problems.
Conclusion
Acceleration is the rate of change of velocity and allows us to depict the motion of objects with irresolute velocities. Information technology is important to call back that dispatch is a vector quantity with both magnitude and direction. To place if an object's acceleration is positive or negative, we need to consider both if the object is speeding up or slowing down and the direction the object is moving.
Source: https://www.albert.io/blog/how-to-find-acceleration/
Posted by: fullerondowde.blogspot.com


0 Response to "How To Find The Speed Of An Object"
Post a Comment